

分析 (1)①由条件可证明Rt△ADC≌Rt△BEC,可证得BE=AD,再利用直角三角形的性质可证明BE=2CF;②由直角三角形的性质可得CF=DF,可证明∠FCD=∠ADC,可证得∠EBC+∠FCD=90°,可证明结论;
(2)延长CF到M,使FM=FC,连接AM,DM,可证明四边形ACDM为平行四边形,进一步可证明△MAC≌△ECB,则可得MC=BE,可证得BE=2CF,再结合∠ACB=90°,可证明BE⊥CF.
解答 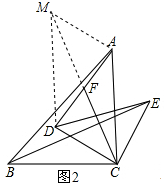 (1)证明:
(1)证明:
①∵△ABC和△DEC都是等腰直角三角形,
∴BC=AC,CD=CE,∠ACB=∠ECD=90°,
在△BCE和△ACD中
$\left\{\begin{array}{l}{BC=AC}\\{∠BCE=∠ACD}\\{CE=CD}\end{array}\right.$
∴△BCE≌△ACD(SAS),
∴BE=AD,∠EBC=∠DAC,
∵F为线段AD的中点,
∴CF=AF=DF=$\frac{1}{2}$AD
∴BE=2CF;
②∵AF=CF,
∴∠DAC=∠FCA,
∵∠BCF+∠ACF=90°,
∴∠BCF+∠EBC=90°,
即BE⊥CF;
(2)旋转一个锐角后,(1)中的关系依然成立.
证明:如图2,延长CF到M,使FM=FC,连接AM,DM,
又AF=DF,
∴四边形AMDC为平行四边形
∴AM=CD=CE,∠MAC=180°-∠ACD,
∠BCE=∠BCA+∠DCE-∠ACD=180°-∠ACD,
即∠MAC=∠BCE,
在△MAC和△ECB中
$\left\{\begin{array}{l}{AC=BC}\\{∠MAC=∠BCE}\\{AM=CE}\end{array}\right.$
∴△MAC≌△ECB(SAS),
∴CM=BE;∠ACM=∠CBE,
∴BE=CM=2CF;
∴∠CBE+∠BCM=∠ACM+∠BCM=90°,
即BE⊥CF.
点评 本题主要考查三角形的综合应用,涉及知识点有等腰三角形、直角三角形的性质、全等三角形的判定和性质、平行四边形的判定和性质等.在(1)中注意直角三角形斜边上的中线等于斜边的一半,在(2)中构造三角形全等是解题的关键.本题知识点较多,但是思路清晰,难度不大,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△A1B1A2,△A2B2A3,△A3B3A4,…△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上,已知OA2=1,则OA2016的长为( )
如图,△A1B1A2,△A2B2A3,△A3B3A4,…△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上,已知OA2=1,则OA2016的长为( )| A. | 22013 | B. | 22014 | C. | 22015 | D. | 22016 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{1}{2}}$ | B. | $\sqrt{0.2}$ | C. | $\sqrt{7}$ | D. | $\sqrt{(-3)^{2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com