
【题目】如图,PA为⊙O的切线,A为切点.过A作OP的垂线AB,垂足为点C,交⊙O于点B.延长BO与⊙O交于点D,与PA的延长线交于点E.
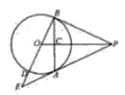
(1)求证:PB为⊙O的切线;(2)若tan∠ABE=![]() ,求sinE的值.
,求sinE的值.
【答案】
(1)证明:连接OA
∵PA为⊙O的切线,
∴∠PAO=90°
∵OA=OB,OP⊥AB于C
∴BC=CA,PB=PA
∴△PBO≌△PAO
∴∠PBO=∠PAO=90°
∴PB为⊙O的切线
(2)解法1:连接AD,∵BD是直径,∠BAD=90°
由(1)知∠BCO=90°
∴AD∥OP
∴△ADE∽△POE
∴EA/EP=AD/OP 由AD∥OC得AD=2OC ∵tan∠ABE="1/2 " ∴OC/BC=1/2,设OC=t,则BC=2t,AD=2t由△PBC∽△BOC,得PC=2BC=4t,OP=5t
∴EA/EP=AD/OP=2/5,可设EA=2m,EP=5m,则PA=3m
∵PA=PB∴PB=3m
∴sinE=PB/EP=3/5
(2)解法2:连接AD,则∠BAD=90°由(1)知∠BCO=90°∵由AD∥OC,∴AD=2OC ∵tan∠ABE=1/2,∴OC/BC=1/2,设OC=t,BC=2t,AB=4t由△PBC∽△BOC,得PC=2BC=4t,
∴PA=PB=2![]() t 过A作AF⊥PB于F,则AF·PB=AB·PC
t 过A作AF⊥PB于F,则AF·PB=AB·PC
∴AF=![]() t 进而由勾股定理得PF=
t 进而由勾股定理得PF=![]() t
t
∴sinE=sin∠FAP=PF/PA=3/5
【解析】略


科目:初中数学 来源: 题型:
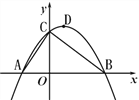
【题目】如图,已知点A的坐标为(-2,0),直线![]() 与x轴、y轴分别交于点B和点C,连接AC,顶点为D的抛物线
与x轴、y轴分别交于点B和点C,连接AC,顶点为D的抛物线![]() 过A、B、C三点.
过A、B、C三点.
(1)求抛物线的解析式及顶点D的坐标;
(2)设抛物线的对称轴DE交线段BC于点E,P是第一象限内抛物线上一点,过点P作x轴的垂线,交线段BC于点F,若四边形DEFP为平行四边形,求点P的坐标.
(3)设点M是线段BC上的一动点,过点M作MN∥AB,交AC于点N,点Q从点B出发,以每秒1个单位长度的速度沿线段BA向点A运动,运动时间为t(秒),当t(秒)为何值时,存在△QMN为等腰直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC与BD相交于点O,CE//BD,DE//AC.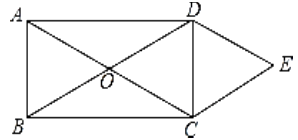
(1)求证:四边形OCED是菱形;
(2)当CD=6,DE=5,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+b中,y随x的增大而增大,b<0,则这个函数的图象不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xOy中,点P的坐标为( ![]() ),点Q的坐标为
),点Q的坐标为 ![]() ,且
,且 ![]() ,
, ![]() ,若P,Q为某个矩形的两个顶点,且该矩形的一组对边与某条坐标轴平行,则称该矩形为点P,Q的“相关矩形”,图2及图3中点A的坐标为(4,3).
,若P,Q为某个矩形的两个顶点,且该矩形的一组对边与某条坐标轴平行,则称该矩形为点P,Q的“相关矩形”,图2及图3中点A的坐标为(4,3).
(1)若点B的坐标为(-2,0),则点A,B的“相关矩形”的面积为;
(2)点C在y轴上,若点A,C的“相关矩形”的面积为8,求直线AC的解析式;
(3)如图3,直线 ![]() 与x轴交于点M,与y轴交于点N,在直线MN上是否存在点D,使点A,D的“相关矩形”为正方形,如果存在,请求出点D的坐标,如果不存在,请说明理由.
与x轴交于点M,与y轴交于点N,在直线MN上是否存在点D,使点A,D的“相关矩形”为正方形,如果存在,请求出点D的坐标,如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线AC、BD相交于点O,分别作BE⊥AC于E,DF⊥AC于F,已知OE=OF,CE=AF.
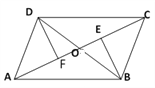
(1)求证:△BOE≌△DOF;
(2)若![]() ,则四边形ABCD是什么特殊四边形?请说明理由.
,则四边形ABCD是什么特殊四边形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春天来了!有一群小朋友在草地上开心的玩耍,所有的男生都戴黄帽子,女生都带红帽子,但有趣的事:在每个男生看来,黄帽子和红帽子一样多, 在每个女生看来, 黄帽子是红帽子的2倍 ,则男生和女生共有_______人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市甲、乙两个汽车销售公司,去年一至十月份每月销售同种品牌汽车的情况如图所示: 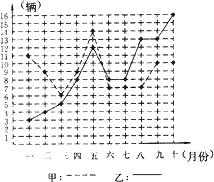
(1)请你根据上图填写下表:
销售公司 | 平均数 | 方差 | 中位数 | 众数 |
甲 | 5.2 | 9 | ||
乙 | 9 | 17.0 | 8 |
(2)请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析: ①从平均数和方差结合看;
②从折线图上甲、乙两个汽车销售公司销售数量的趋势看(分析哪个汽车销售公司较有潜力).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com