
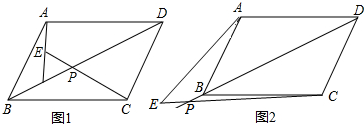
分析 (1)过点C作CM∥AF,利用AAS证明△ABF≌△CDM,得出CM=AF,由∠3=∠CMP,得出CM=CP=AF,那么PC=AF=AE+EF=AE+EP;
(2)过点C作CC′∥AE交BD延长线于C′,直线BD与AE交于K.利用AAS证明△ABK≌△CDC′,得出AK=CC′,进而得出AE+PE=CP.
解答 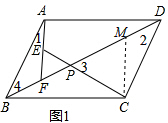 解:(1)PC=PE+AE.理由如下:
解:(1)PC=PE+AE.理由如下:
过点C作CM∥AF,如图1,
∴∠CMP=∠AFP①,
∴∠CMD=∠AFB,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠2=∠4,
∴∠EFP=∠1+∠4,
∵∠CPD=∠BDC+∠BAE,
∴∠3=∠1+∠2,
∴∠EFP=∠3=∠EPF②,
∴EF=EP,
在△ABF和△CDM中,
$\left\{\begin{array}{l}{∠CMD=∠AFB}\\{∠2=∠4}\\{AB=CD}\end{array}\right.$,
∴△ABF≌△CDM(AAS),
∴CM=AF,
∴∠3=∠CMP,
∴CM=CP=AF,
∴PC=AF=AE+EF=AE+EP;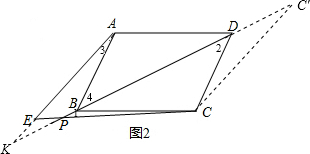 (2)(1)中的结论还成立,理由如下:
(2)(1)中的结论还成立,理由如下:
过点C作CC′∥AE交BD延长线于C′,直线BD与AE交于K,如图2.
在?ABCD中,∵AB∥CD,
∴∠2=∠4.
∵∠4=∠3+∠K,∠2=∠1+∠3,
∴∠K=∠1,
∵∠1=∠EPK,
∴∠K=∠EPK,
∴EK=EP,
∴AK=AE+EK=AE+EP.
∵CC′∥AK,
∴∠K=∠C′=∠1,
∴CP=CC′.
在△ABK与△CDC′中,
$\left\{\begin{array}{l}{∠K=∠C′}\\{∠ABK=∠CDC′}\\{AB=CD}\end{array}\right.$,
∴△ABK≌△CDC′(AAS),
∴AK=CC′,
∴AE+PE=CP.
点评 本题考查了平行四边形的性质,平行线的性质,等腰三角形、全等三角形的判定与性质,准确作出辅助线是解题的关键.


科目:初中数学 来源: 题型:填空题
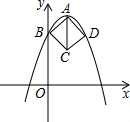 如图,在平面直角坐标系中,正方形ABCD的三个顶点A、B、D均在抛物线y=ax2-4ax+3(a<0)上.若点A是抛物线的顶点,点B是抛物线与y轴的交点,则AC长为4.
如图,在平面直角坐标系中,正方形ABCD的三个顶点A、B、D均在抛物线y=ax2-4ax+3(a<0)上.若点A是抛物线的顶点,点B是抛物线与y轴的交点,则AC长为4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
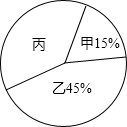 某校图书管理员清理课外书籍时,将其中甲、乙、丙三类书籍的有关数据制成如图不完整的统计图,已知甲类书有30本,则丙类书的本数是( )
某校图书管理员清理课外书籍时,将其中甲、乙、丙三类书籍的有关数据制成如图不完整的统计图,已知甲类书有30本,则丙类书的本数是( )| A. | 80 | B. | 144 | C. | 200 | D. | 90 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
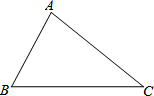 (1)如图,试用直尺与圆规在平面内确定一点O,使得点O到△ABC的两边AB、AC的距离相等,并且点O到B、C两点的距离也相等.(不写作法,但需保留作图痕迹)
(1)如图,试用直尺与圆规在平面内确定一点O,使得点O到△ABC的两边AB、AC的距离相等,并且点O到B、C两点的距离也相等.(不写作法,但需保留作图痕迹)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com