
如图,△ABC中,∠B=90°,AB=6cm,BC=12cm.点P从点A开始,沿AB边向点B 以每秒1cm的速度移动;点Q从点B开始,沿着BC边向点C以每秒2cm的速度移动.如果P,Q 同时出发,问经过几秒钟△PBQ的面积最大?最大面积是多少?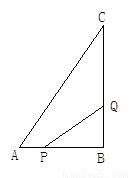
第3秒钟时△PBQ的面积最大,最大值是9cm2
【解析】
试题分析:设第t秒时,△PBQ的面积为ycm2,先根据路程=速度×时间分别表示出AP、PB、BQ,再根据三角形的面积公式即可得到函数关系式,最后根据二次函数的性质即得结果.
设第t秒时,△PBQ的面积为ycm2.
∵AP=tcm,
∴PB=(6-t)cm;
又BQ=2t.
∴y=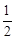 PB·BQ=
PB·BQ=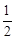 (6-t)·2t=(6-t)t=-t2+6t=-(t-3)2+9,
(6-t)·2t=(6-t)t=-t2+6t=-(t-3)2+9,
当t=3时,y有最大值9.
故第3秒钟时△PBQ的面积最大,最大值是9cm2.
考点:二次函数的应用
点评:配方法在二次函数的问题中极为重要,尤其在中考中比较常见,往往出现在中考压轴题中,难度不大,要特别注意.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
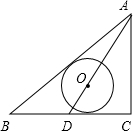 如图△ABC中,∠C=90°,AC=6,AB=10,D是BC边的中点,以AD上一点O为圆心的圆与AB,BC都相切,则⊙O的半径为( )
如图△ABC中,∠C=90°,AC=6,AB=10,D是BC边的中点,以AD上一点O为圆心的圆与AB,BC都相切,则⊙O的半径为( )A、
| ||
B、
| ||
C、
| ||
| D、2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图△ABC中,∠A=78°,AB=AC,P为△ABC内一点,连BP,CP,使∠PBC=9°,∠PCB=30°,连PA,则∠BAP的度数为
如图△ABC中,∠A=78°,AB=AC,P为△ABC内一点,连BP,CP,使∠PBC=9°,∠PCB=30°,连PA,则∠BAP的度数为查看答案和解析>>
科目:初中数学 来源: 题型:
 如图△ABC中,∠ABC=20°,外角∠ABF的平分线与CA边的延长线交于点D,外角∠EAC的平分线交BC边的延长线于点H,若∠BDA=∠DAB,则∠AHC=( )度.
如图△ABC中,∠ABC=20°,外角∠ABF的平分线与CA边的延长线交于点D,外角∠EAC的平分线交BC边的延长线于点H,若∠BDA=∠DAB,则∠AHC=( )度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com