
分析 (1)设甲每小时分别行驶3x千米,乙每小时分别行驶2x千米,依据“甲车比乙车早到了$\frac{2}{3}$小时”列出方程并解答,注意:分式方程需要验根;
(2)设乙车在B地停留a小时,根据已知条件列出不等式并解答.
解答 解:(1)设甲每小时分别行驶3x千米,乙每小时分别行驶2x千米,$\frac{120}{3x}$=$\frac{120}{2x}$-$\frac{2}{3}$.
解得:x=30.
经检验,x=30是原方程的解.
则3x=90,2x=60.
答:设甲每小时分别行驶90千米,乙每小时分别行驶60千米;
(2)设乙车在B地停留a小时,则
120×2÷90=$\frac{8}{3}$(小时),
($\frac{8}{3}$-a)×60≥120+20,
解得:a≤$\frac{1}{3}$.
答:乙车在B地停留最多不能超过$\frac{1}{3}$小时.
点评 本题考查了一元一次不等式的应用,分式方程的应用.利用分式方程解应用题时,一般题目中会有两个相等关系,这时要根据题目所要解决的问题,选择其中的一个相等关系作为列方程的依据,而另一个则用来设未知数.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1:$\sqrt{3}$ | B. | $\sqrt{3}:1$ | C. | 2:$\sqrt{3}$ | D. | $\sqrt{3}:2$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
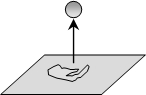 如图,把一个小球垂直向上抛出,则下列描述该小球的运动速度v(单位:m/s)与运动时间t(单位s)关系的函数图象中,正确的是( )
如图,把一个小球垂直向上抛出,则下列描述该小球的运动速度v(单位:m/s)与运动时间t(单位s)关系的函数图象中,正确的是( )| A. | 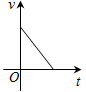 | B. | 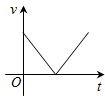 | C. | 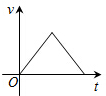 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2+x4=x6 | B. | x6÷x3=x2 | ||
| C. | $\frac{-a-b}{a+b}$=-1 | D. | $\frac{b}{{a}^{2}-{b}^{2}}$÷(1-$\frac{a}{a+b}$)=-$\frac{1}{a-b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com