
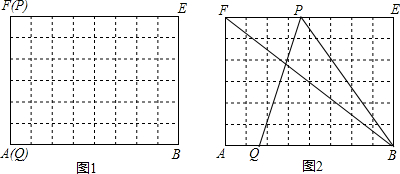
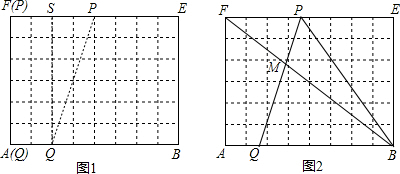
 解:(1)如图1.
解:(1)如图1.| 62+82 |
| QB |
| FB |
| MB |
| AB |
| 8-t |
| 10 |
| x |
| 8 |
| FM |
| FE |
| FD |
| FB |
| 10-x |
| 8 |
| 2t |
| 10 |
| 9 |
| 2 |
| 8 |
| 2 |
| 9 |
| 2 |
| 8 |
| 3 |
| 7 |
| 4 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(广西区南宁卷)数学 题型:选择题
如图5,在正方形ABCD中,E、F分别是边BC、CD的中点,AE交BF于点H,CG∥AE交BF于点G。下列结论:①tan∠HBE=cot∠HEB ② 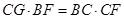 ③BH=FG ④
③BH=FG ④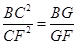 .其中正确的序号是
.其中正确的序号是
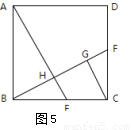
A. ①②③ B. ②③④ [来源:学_科_网Z_X_X_K] C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2004年全国中考数学试题汇编《图形的对称》(03)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2004年河北省中考数学试卷(课标卷)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com