
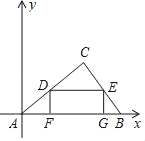
����Ŀ����ͼ����Rt��ABC�У���C��90����AC��4��BC��3���Ե�AΪԭ�㽨��ƽ��ֱ������ϵ��ʹAB��x���������ϣ���D��AC���ϵ�һ�����㣬DE��AB��BC��E��DF��AB��F��EG��AB��G�����½��ۣ�
����AFD�ס�DCE�ס�EGB��
�ڵ�DΪAC���е�ʱ����AFD�ա�DCE��
�۵�C������Ϊ��3.2��2.4����
�ܽ���ABC��AC���ڵ�ֱ�߷��۵�ԭ����ƽ�棬��B�Ķ�Ӧ��B1������Ϊ��1.6��4.8����
�ݾ���DEGF��������Ϊ3������Щ��������ȷ����_____��ֻ����ţ�
���𰸡��٢ۢ�
��������
����ȷ���������Ƕ�Ӧ��ȵ��������������Ƽ����жϣ�
�ڴ�����б�߲���ȼ����жϣ�
����ȷ�������C���꼴���жϣ�
�ܴ��������B1�����жϣ�
����ȷ������֤���ı���DEGF�Ǿ��Σ��Ƴ�DF=EG��DE=FG����DF=EG=x���������κ��������ö��κ��������ʼ����ж�.
��ͼ����CH��AB��H��
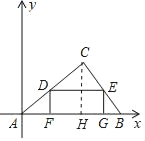
��DF��AB��F��EG��AB��G��
���AFD����DCE����EGB��90����
��DE��AB��
���CDE����DAF����CED����EBG��
���AFD�ס�DCE�ס�EGB���ʢ���ȷ��
��AD��CDʱ����DE��CD��
��DE��AD��
���AFD����DCE��ȫ�ȣ��ʢڴ���
��Rt��ACB����AC��4��BC��3��
��AB��5��CH��![]() 4��
4��
��AH��![]() ��3.2��
��3.2��
��C��3.2��2.4�����ʢ���ȷ��
����ABC��AC���ڵ�ֱ�߷��۵�ԭ����ƽ�棬��B�Ķ�Ӧ��B1����B1Ϊ��m��n����
����![]() ��3.2��m��1.4��
��3.2��m��1.4��
![]() ��2.4��n��4.8��
��2.4��n��4.8��
��B1��1.4��4.8�����ʢܴ���
��DF��AB��F��EG��AB��G��
��DF��EG��
��DE��AB��
���ı���DEGF��ƽ���ı��Σ�
�ߡ�DFG��90����
���ı���DEGF�Ǿ��Σ�
��DF��EG��DE��FG����DF��EG��x����AF=![]() x��BG��
x��BG��![]() x��
x��
��DE��FG��5��![]() x��
x��![]() x��5��
x��5��![]() x��
x��
��S����DEGF��x��5��![]() x������
x������![]() x2+5x��
x2+5x��
�ߩ�![]() ��0��
��0��
��S�����ֵ��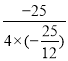 ��3���ʢ���ȷ��
��3���ʢ���ȷ��
������������ȷ���У��٢ۢݣ�
�ʴ�Ϊ�٢ۢݣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
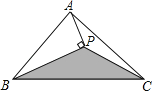
����Ŀ����ͼ����ABC�����Ϊ10cm2��BPƽ�֡�ABC��AP��BP������ΪP������CP��������������һ��M�����M������BPC�ڣ������߽磩�ĸ���Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������![]() ��ͼ�������AOBC�ı�AC��BC�ֱ��ཻ�ڵ�E��F����C������Ϊ��4��3������CEF��EF���ۣ�C��ǡ������OB�ϵĵ�D������k��ֵΪ��������
��ͼ�������AOBC�ı�AC��BC�ֱ��ཻ�ڵ�E��F����C������Ϊ��4��3������CEF��EF���ۣ�C��ǡ������OB�ϵĵ�D������k��ֵΪ��������
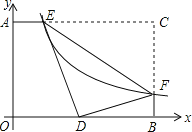
A. ![]() B. 6C. 3D.
B. 6C. 3D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��0��2������x����ȡһ��B������AB����AΪԲ�ģ����ⳤΪ�뾶�������ֱ�OA��AB�ڵ�M��N������M��NΪԲ�ģ�����![]() MN�ij�Ϊ�뾶�������������ڵ�D������AD���ӳ���x���ڵ�P������OPA����OAB���ƣ����P������Ϊ��������
MN�ij�Ϊ�뾶�������������ڵ�D������AD���ӳ���x���ڵ�P������OPA����OAB���ƣ����P������Ϊ��������
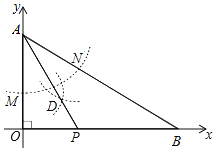
A. ��1��0��B. ��![]() ��0��C. ��
��0��C. ��![]()
![]() ��0��D. ��2
��0��D. ��2![]() ��0��
��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��֣���д���������̬�ֳ���ʵʩ�����Ѿ���̨����2019��5�µף�����������Ҫ�ﵽ����������̬�ֳ��б�������ָ��Ҫ��֣��������·�ƹ���Ҫ����85%�����ƽ��˻�У�֣����ijС����������A��B������ľ�����������飬��ȡ��Ϣ���£��������A����ľ40�ã�B����ľ60�ã��踶��11400Ԫ���������A����ľ50�ã�B����ľ50�ã��踶��10500Ԫ��
���� | ������������50�� | ��������������50�� |
A | ԭ������ | �������� |
B | ԭ������ | �Ծ������� |
��1��A����ľ��B����ľ�ĵ��۸�����Ԫ��
��2���������㣬��Ҫ����A��B������ľ��100�ã�����B����ľ������������A����ľ������֮һ����ι������٣����ٷ����Ƕ���Ԫ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽�ѧ����������ë�������������·ֱ���A��B��C��D��ʾ�������������˶���ϲ���������ȫ��ѧ�������˳������飨ÿλѧ��ֻ��ѡһ����ϲ�����˶�������������������Ƴ�����������������ͳ��ͼ��
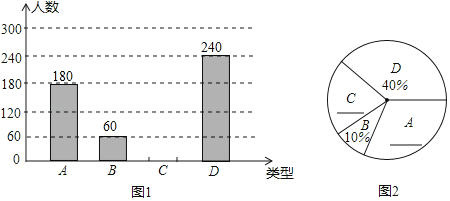
�����������Ϣ�ش��������⣺
��1�����βμӳ��������ѧ������ ���ˣ�
��2����ȫ����ͳ��ͼ��
��3�����ӱ��βμӳ��������ѧ������ȡ1�ˣ������ϲ��������ĸ������������ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����˷ɻ���A��ˮƽ����10����B�㣬�ڵ�����C�����A�㡢B������Ƿֱ�Ϊ45����75������֪���˷ɻ��ķ����ٶ�Ϊ80��/�룬��������˷ɻ��ķ��и߶�Ϊ_____��
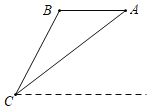
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С������ͼ��ʾ�Ķ��κ���y=ax2+bx+c��a��0����ͼ���У��۲�ó�������������Ϣ��
��ab��0����a+b+c��0����b+2c��0����a��2b+4c��0����![]() ��
��
����Ϊ������ȷ��Ϣ�ĸ�����
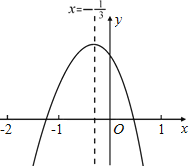
A��2�� B��3�� C��4�� D��5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У���O�ڶԽ���AC�ϣ���OA�ij�Ϊ�뾶����O��AD��AC�ֱ��ڵ�E��F������ACB=��DCE��
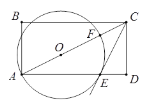
��1���ж�ֱ��CE����O��λ�ù�ϵ����֤����Ľ��ۣ�
��2����tan��ACB=![]() ��BC=4������O�İ뾶��
��BC=4������O�İ뾶��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com