
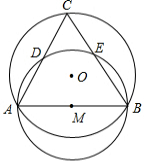
 如图,⊙O的半径为2,弦AB的长为2$\sqrt{3}$,以AB为直径作⊙M,点C是优弧$\widehat{AB}$上的一个动点,连接AC、BC,分别交⊙M于点D、E,则线段CD的最大值为2.
如图,⊙O的半径为2,弦AB的长为2$\sqrt{3}$,以AB为直径作⊙M,点C是优弧$\widehat{AB}$上的一个动点,连接AC、BC,分别交⊙M于点D、E,则线段CD的最大值为2. 分析 如图,连接OA、OB、BD.首先证明∠BDC=90°,∠CBD=30°,由此推出CD=$\frac{1}{2}$BC,欲求CD的最大值,只要求出⊙O的弦BC的最大值即可.
解答 解:如图,连接OA、OB、BD.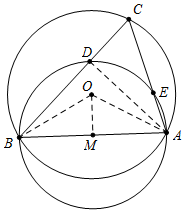
∵OA=OB=2,AM=BM=$\sqrt{3}$.,
∴OM⊥AB,∠AOM=∠BOM,
∴sin∠AOM=$\frac{AM}{AO}$=$\frac{\sqrt{3}}{2}$,
∴∠AOM=60°,
∴∠AOB=2∠AOM=120°,
∴∠C=$\frac{1}{2}$∠AOC=60°,
∵AB是⊙M的直径,
∴∠ADM=90°,
在Rt△BCD中,∵∠CDB=90°,∠CBD=30°,
∴CD=$\frac{1}{2}$BC,
∴欲求CD的最大值,只要求出⊙O的弦BC的最大值,
∵⊙O的直径为4,
∴弦BC的最大值为4,
∴CD的最大值为2.
故答案为2.
点评 本题考查圆综合题、垂径定理、圆周角定理、直角三角形的30度角性质等知识,解题的关键是学会添加辅助线,学会用转化的思想思考问题,本题的突破点是证明CD=$\frac{1}{2}$BC,求出BC的最大值,属于中考填空题中的压轴题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 如图,是由每个边长都是1的小正方形构成的网格,点O,A,B,M均为格点,P为线段OM上的一个动点.
如图,是由每个边长都是1的小正方形构成的网格,点O,A,B,M均为格点,P为线段OM上的一个动点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD为矩形,点E在AD边上,DE=4AE,EF∥AC,交CD边于点F,连接BE,若∠DEF=2∠ABE,BE=2$\sqrt{3}$,则线段EF的长为$\frac{24}{5}$.
如图,四边形ABCD为矩形,点E在AD边上,DE=4AE,EF∥AC,交CD边于点F,连接BE,若∠DEF=2∠ABE,BE=2$\sqrt{3}$,则线段EF的长为$\frac{24}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
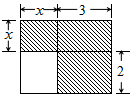 下面四个整式中,不能表示图中阴影部分面积的是( )
下面四个整式中,不能表示图中阴影部分面积的是( )| A. | (x+3)(x+2)-2x | B. | x(x+3)+6 | C. | 3(x+2)+x2 | D. | x2+5x |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解一批圆珠笔的使用寿命 | |
| B. | 了解全国八年级学生身高的现状 | |
| C. | 检查发射神舟11号飞船的运载火箭的各零部件 | |
| D. | 考察世界人们保护海洋的意识 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=2(x+1)2-2 | B. | y=2(x-1)2-2 | C. | y=2(x-2)2-1 | D. | y=2(x+2)2+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com