
已知矩形ABCD和点P,当点P在BC上任一位置(如图(1)所示)时,易证得结论:PA2+PC2=PB2+PD2,请你探究:当点P分别在图(2)、图(3)中的位置时,PA2、PB2、PC2和PD2、又有怎样的数量关系?请你写出对上述两种情况的探究结论,并利用图(2)证明你的结论.
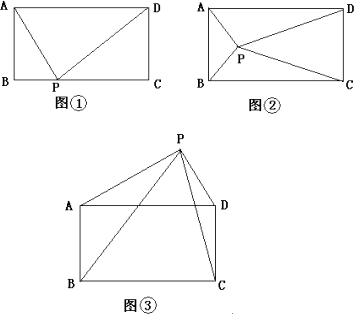
答:对图(2)的探究结论为________________________.
对图(3)的探究结论为________________________________.
证明:如图(2)
|
结论均是PA2+PC2=PB2+PD2(图2 2分,图3 1分) 证明:如图2过点P作MN⊥AD于点M,交BC于点N, 因为AD∥BC,MN⊥AD,所以MN⊥BC 在Rt△AMP中,PA2=PM2+MA2 在Rt△BNP中,PB2=PN2+BN2 在Rt△DMP中,PD2=DM2+PM2 在Rt△CNP中,PC2=PN2+NC2 所以PA2+PC2=PM2+MA2+PN2+NC2 PB2+PD2=PM2+DM2+BN2+PN2 因为MN⊥AD,MN⊥NC,DC⊥BC,所以四边形MNCD是矩形 所以MD=NC,同理AM=BN, 所以PM2+MA2+PN2+NC2=PM2+DM2+BN2+PN2 即PA2+PC2=PB2+PD2 |


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
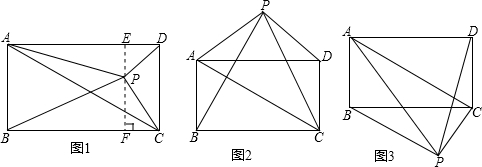
已知矩形ABCD和点P,当点P在图1中的位置时,则有结论:S△PBC=S△PAC+
S△PCD 理由:过点P作EF垂直BC,分别交AD、BC于E、F两点.
∵ S△PBC+S△PAD=BC·PF+AD·PE=BC(PF+PE)=BC·EF=S矩形ABCD
又∵ S△PAC+S△PCD+S△PAD=S矩形ABCD
∴S△PBC+S△PAD=S△PAC+S△PCD+S△PAD.
∴ S△PBC=S△PAC+S△PCD.
请你参考上述信息,当点P分别在图2、图3中的位置时,S△PBC、S△PAC、S△PCD又
有怎样的数量关系?请写出你对上述两种情况的猜想,并选择其中一种情况的猜想给
予证明.

查看答案和解析>>
科目:初中数学 来源:2011-2012学年辽宁大石桥市九年级中考模拟(四)数学试卷(解析版) 题型:解答题
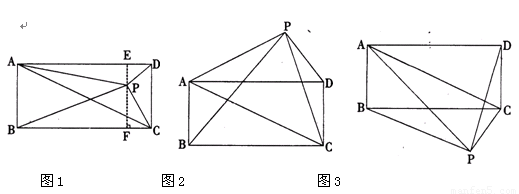
已知矩形ABCD和点P,当点P在图1中的位置时,则有结论:S△PBC=S△PAC+
S△PCD 理由:过点P作EF垂直BC,分别交AD、BC于E、F两点.
∵ S△PBC+S△PAD=BC·PF+AD·PE=BC(PF+PE)=BC·EF=S矩形ABCD
又∵ S△PAC+S△PCD+S△PAD=S矩形ABCD
∴S△PBC+S△PAD=S△PAC+S△PCD+S△PAD.
∴ S△PBC=S△PAC+S△PCD.
请你参考上述信息,当点P分别在图2、图3中的位置时,S△PBC、S△PAC、S△PCD又
有怎样的数量关系?请写出你对上述两种情况的猜想,并选择其中一种情况的猜想给
予证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com