
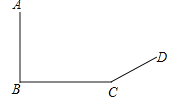
【题目】如图,数学兴趣小组想测量电线杆AB的高度,他们发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4 m,BC=10 m,CD与地面成30°角,且此时测得高1 m的标杆的影长为2 m,则电线杆的高度为________m(结果保留根号).
【答案】(7+![]() )
)
【解析】过D作DE⊥BC的延长线于E,连接AD并延长交BC的延长线于F,根据直角三角形30°角所对的直角边等于斜边的一半求出DE,再根据勾股定理求出CE,然后根据同时同地物高与影长成正比列式求出EF,再求出BF,再次利用同时同地物高与影长成正比列式求解即可.
如图,过D作DE⊥BC的延长线于E,连接AD并延长交BC的延长线于F,
∵CD=4 m,CD与地面成30°角,∴DE=![]() CD=
CD=![]() ×4=2 m,
×4=2 m,
根据勾股定理得:CE=![]() =
=![]() =2
=2![]() m,
m,
∵1 m杆的影长为2 m,∴![]() =
=![]() ,∴EF=2DE=2×2=4 m,
,∴EF=2DE=2×2=4 m,
∴BF=BC+CE+EF=10+2![]() +4=(14+2
+4=(14+2![]() )m,
)m,
∴![]() =
=![]() ,∴AB=
,∴AB=![]() (14+2
(14+2![]() )=(7+
)=(7+![]() )m.
)m.
故答案为:(7+![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某通讯公司就上宽带网推出A,B,C三种月收费方式.这三种收费方式每月所需的费用y(元![]() 与上网时间x(h)的函数关系如图所示,则下列判断错误的是
与上网时间x(h)的函数关系如图所示,则下列判断错误的是![]()
![]()
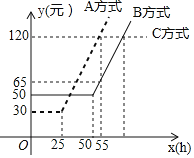
A. 每月上网时间不足25h时,选择A方式最省钱 B. 每月上网费用为60元时,B方式可上网的时间比A方式多
C. 每月上网时间为35h时,选择B方式最省钱 D. 每月上网时间超过70h时,选择C方式最省钱
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们都知道,![]() 表示4与-2的差的绝对值,实际上也可理解为4与-2两数在数轴上所对应的两点之间的距离,同理
表示4与-2的差的绝对值,实际上也可理解为4与-2两数在数轴上所对应的两点之间的距离,同理![]() 也可理解为
也可理解为![]() 与3两数在数轴上所对应的两点之间的距离,
与3两数在数轴上所对应的两点之间的距离,![]() 就表示
就表示![]() 在数轴上对应的点到-1的距离,由上面绝对值的几何意义,解答下列问题:
在数轴上对应的点到-1的距离,由上面绝对值的几何意义,解答下列问题:
(1)求![]() .
.
(2)若![]() ,则
,则![]() .
.
(3)请你找出所有符合条件的整数![]() ,使得
,使得![]() .
.
(4)求![]() 的最小值,并写出此时
的最小值,并写出此时![]() 的取值情况.
的取值情况.
(5)已知![]() ,求
,求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 分别为数轴上的两点,
分别为数轴上的两点,![]() 点对应的数为-20,
点对应的数为-20,![]() 点对应的数为100.
点对应的数为100.

(1)请写出![]()
![]() 中点
中点![]() 所对应的数;
所对应的数;
(2)现有一只电子蚂蚊![]() 从
从![]() 点出发,以6单位秒的速度向左运动,同时另一只电子蚂蚁
点出发,以6单位秒的速度向左运动,同时另一只电子蚂蚁![]() 恰好从
恰好从![]() 点出发,以4单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的
点出发,以4单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的![]() 点相遇,求
点相遇,求![]() 点对应的数.
点对应的数.
(3)若当电子蚂蚁![]() 从
从![]() 点出发时,以6单位/秒的速度向左运动,同时另一只电子蚂蚁
点出发时,以6单位/秒的速度向左运动,同时另一只电子蚂蚁![]() 恰好从
恰好从![]() 点出发,以4单位/秒的速度也向左运动,设两只电子蚂蚁在数轴上的
点出发,以4单位/秒的速度也向左运动,设两只电子蚂蚁在数轴上的![]() 点相遇,求
点相遇,求![]() 点对应的数.
点对应的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是线段AB的中点,Q为线段PB上一点,分别以AQ、AP、PQ、QB为一边作正方形,其面积对应地记作SACDQ,SAEFP,SPGHQ,SQIJB,设AP=m,QB=n,
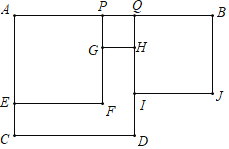
(1)用含有m,n的代数式表示正方形ACDQ的面积SACDQ.
(2)SACDQ+SQIJB与SAEFP+SPGHQ具有怎样的数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=5,BC=6,AD是BC边上的中线且AD=4,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为_____.
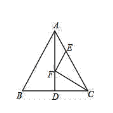
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b=ab2﹣2ab+b.
如:2☆(﹣3)=2×(﹣3)2﹣2×2×(﹣3)+(﹣3)=27
(1)求(﹣4)☆7的值;
(2)若(1﹣3x)☆(﹣4)=32,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我们的课本第142页“4.4课题学习”中,有包装纸盒的设计制作方法.这里的右图,是设计师为“XX快递”设计的长方体包装盒的轮廓草图,其中长30CM、宽20CM、高18CM,正面有“快递”字样,上面有“上”字样,棱AB是上盖的掀开处,棱CD是粘合处.请你想想,如何制作这个包装盒,然后完善下面的制作步骤.
步骤1:在符合尺寸规格的硬纸板上,画出这个长方体的展开图(草图).注意,要预留出黏合处,并适当剪去棱角.
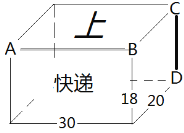
步骤2:在你上面画出的展开草图上,标出对应的A、B、C、D的位置,标出长30CM、宽20CM、高18CM所在线段,并把“上”和“快递”标注在所在面的位置上.
步骤3:裁下展开图,折叠并粘好黏合处,得到长方体包装盒.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com