
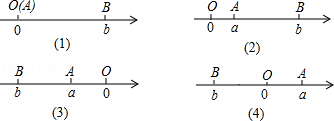
分析 ①根据数轴上A,B两点之间的距离|AB|=|a-b|回答即可;
②根据数轴上A,B两点之间的距离|AB|=|a-b|回答即可;
③|x+1|+|x-3|的最小值,意思是x到-1的距离与到3的距离之和最小,那么x应在-1和3之间的线段上.
④分三种情况讨论即可求得.
解答 解:①|2-5|=3,|-2-(-5)|=3,|1-(-3)|=4;
②|x-(-1)|=|x+1|,
如果AB=2,则x+1=±2,
解得x=1或-3;
③若|x+1|+|x-2|取最小值,那么表示x的点在-1和2之间的线段上,
所以-1≤x≤2.
④若x+1>0,x-2>0,则(x+1)+(x-2)=5,解得x=3,
若x+1<0,x-2<0,则-(x+1)-(x-2)=5,解得x=-2,
若x+1和x-2异号,则等式不成立,
所以当x=3或-2时,|x+1|+|x-2|=5.
故答案为:3,3,4;|x+1|,1或-3;-1≤x≤2;3或-2.
点评 本题主要考查了数轴和绝对值,掌握数轴上两点间的距离=两个数之差的绝对值.


科目:初中数学 来源: 题型:选择题
| A. | 扩大为原来的2倍 | B. | 扩大为原来的4倍 | C. | 缩小为原来的2倍 | D. | 不变 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
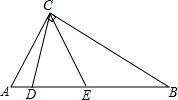 如图,在Rt△ABC中,AC=6,BC=8,D,E为斜边AB上的两个点,且BD=BC,AE=AC,则△DCE的外接圆的半径是2$\sqrt{2}$.
如图,在Rt△ABC中,AC=6,BC=8,D,E为斜边AB上的两个点,且BD=BC,AE=AC,则△DCE的外接圆的半径是2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 点C 在⊙A内 | B. | 点C在⊙A上 | C. | 点C在⊙A外 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com