
【题目】为了解某校九年级学生的身高情况,随机抽取了部分学生的身高进行调查,利用所得数据绘成如下统计图表:
频数分布表
身高分组/cm | 频数 | 百分比 |
| 5 | 10% |
| 20% | |
| 15 | 30% |
| 14 | |
| 6 | 12% |
总计 | 100% |
(1)填空:![]() ______;
______;
(2)通过计算补全频数分布直方图;
(3)该校九年级一共有600名学生,估计身高不低于165cm的学生大约有多少人?

【答案】(1)28%;(2)见解析;(3)该校九年级共有600名学生,身高不低于165cm的学生大约有240人
【解析】
(1)用x<155的频数除以所占百分比可以求得调查的学生总数,从而可以求得a的值;
(2)用155≤x<160所占的百分比乘以总人数得到155≤x<160的人数,从而补全频数分布直方图;
(3)用九年级总人数乘以身高不低于165cm的学生所占的百分比即可.
解:(1)由表格可得,调查的总人数为:5÷10%=50,
a=14÷50×100%=28%,
故答案是:28%;
(2)155≤x<160的人数是:50×20%=10(人),补图如下: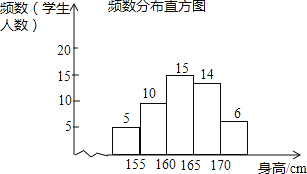
(3)根据题意得:
600×(28%+12%)=600×40%=240(人)
即该校九年级共有600名学生,身高不低于165cm的学生大约有240人.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABDE、CDFI、EFGH的面积分别为25、9、16,△AEH、△BDC、△GFI的面积分别为S1、S2、S3,则S1+S2+S3=_____.
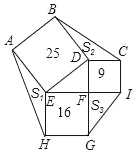
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知数轴上点A、B分别表示a、b,且|b+6|与(a﹣9)2互为相反数,O为原点.
(1)a= ,b= ;
(2)若将数轴折叠点A与表示﹣10的点重合,则与点B重合的点所表示的数为 ;
(3)若点M、N分别从点A、B同时出发,点M以每秒1个单位长度的速度沿数轴向左匀速运动,点N以每秒2个单位长度的速度沿数轴向右匀速运动,N到点A后立刻原速返回,设运动时间为t(t>0)秒.①点M表示的数是 (用含t的代数式表示);②求t为何值时,2MO=MA;③求t为何值时,点M与N相距3个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从仓库O出发在东西街道上运送水果,规定向东为正方向,一次到达的5个销售地点依次分别为A,B,C,D,E,最后回到仓库O,货车行驶的记录(单位:千米)如下:+1,+3,﹣6,﹣1,﹣2,+5.请问:
(1)请以仓库O为原点,向东为正方向,选择适当的单位长度,画出数轴,并标出A,B,C,D,E的位置;
(2)试求出该货车共行驶了多少千米?
(3)如果货车运送的水果以100千克为标准重量,超过的千克数记为正数,不足的千克数记为负数,则运往A,B,C,D,E五个地点的水果重量可记为:
+50,﹣15,+25,﹣10,﹣15,则该货车运送的水果总重量是多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有边长相等的正三角形、正方形、正六进形、正八边形形状的地砖,如果选择其中的两钟铺满平整的地面,那么选择的两种地砖形状不能是( )
A. 正三角形与正方形 B. 正三角形与正六边形
C. 正方形与正六边形 D. 正方形与正八边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(3,﹣6)是二次函数y=ax2上的一点,则这二次函数的解析式是 .
【答案】y=﹣![]() x2
x2
【解析】
试题分析:将点A(3,﹣6)代入y=ax2,利用待定系数法法求该二次函数的解析式即可得﹣6=9a,
解得a=﹣![]() ;因此该二次函数的解析式为:y=﹣
;因此该二次函数的解析式为:y=﹣![]() x2.
x2.
考点:待定系数法求二次函数解析式
【题型】填空题
【结束】
15
【题目】在一个不透明的口袋中装有8个红球和若干个白球,它们除颜色外其它完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在40%附近,则口袋中白球可能有________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一块三角形的空地,其三边的长分别为20m,30m,40m,现要把它分成面积为2:3:4的三部分,分别种植不同的花草,请你设计一种方案,并简单说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,边长为2的正方形ABCD中,点P在AB边上(不与点A、B重合),点Q在BC边上(不与点B、C重合)
第一次操作:将线段PQ绕点Q顺时针旋转,当点P落在正方形上时,记为点M;
第二次操作:将线段QM绕点M顺时针旋转,当点Q落在正方形上时,记为点N;
依次操作下去…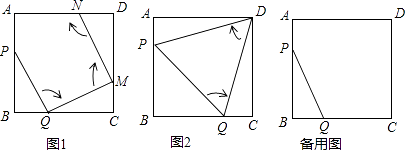
(1)如图2,经过两次操作后得到△PQD、△PQD的形状是 , 求此时线段PQ的长 ;
(2)若经过三次操作可得到四边形PQMN.
①请直接判断四边形PQMN的形状,直接写出此时此刻AP与BQ的数量关系;
②以①中的结论为前提,直接写出四边形PQMN的面积的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填写推理理由:
已知:如图,D,F,E分别是BC,AC,AB上的点,DF∥AB,DE∥AC,

试说明∠EDF=∠A.
解:∵DF∥AB(已知),
∴∠A+∠AFD=180°(____________________).
∵DE∥AC(已知),
∴∠AFD+∠EDF=180°(____________________).
∴∠A=∠EDF(____________________).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com