
 如图所示,已知OB、OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD,若∠AOD=96°,∠MON=68°,求∠BOC的大小.
如图所示,已知OB、OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD,若∠AOD=96°,∠MON=68°,求∠BOC的大小. 分析 由OM平分∠AOB,ON平分∠DOC可知∠AOM=∠BOM,∠DON=∠CON,可知∠BOM+∠CON=∠AOM+∠DON=∠AOD-∠MON,又知∠BOC=∠MON-(∠BOM+∠CON),故可得到∠BOC的度数.
解答 解:∵OM平分∠AOB,ON平分∠DOC,
∴∠AOM=∠BOM,∠DON=∠CON,
∴∠BOM+∠CON=∠AOM+∠DON=∠AOD-∠MON=96°-68°=28°,
∴∠BOC=∠MON-(∠BOM+∠CON)=68°-28°=40°.
点评 本题主要考查了角平分线的定义以及角的和差与运算;熟练掌握角平分线的定义,弄清各个角之间的关系是解决问题的突破口.


科目:初中数学 来源: 题型:选择题
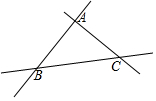 如图是三条两两相交的笔直公路,现欲修建一个加油站,使它到三条公路的距离相等,这个加油站应建在( )
如图是三条两两相交的笔直公路,现欲修建一个加油站,使它到三条公路的距离相等,这个加油站应建在( )| A. | △ABC三边的中线的交点上 | B. | △ABC三边垂直平分线的交点上 | ||
| C. | △ABC三条边高的交点上 | D. | △ABC三内角平分线的交点上 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC的顶点坐标分别为A(4,5),B(2,3),C(5,1).
如图,△ABC的顶点坐标分别为A(4,5),B(2,3),C(5,1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,为估计池塘岸边A、B两点间的距离,在池塘的一侧选取点O,分别取OA、OB的中点M、N,测得MN=40m,则A、B两点间的距离是( )
如图,为估计池塘岸边A、B两点间的距离,在池塘的一侧选取点O,分别取OA、OB的中点M、N,测得MN=40m,则A、B两点间的距离是( )| A. | 20m | B. | 80m | C. | 120m | D. | 160m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
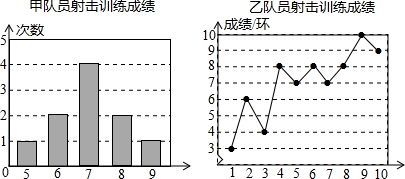
| 平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
| 甲 | 7 | b | 7 | c |
| 乙 | a | 7.5 | 8 | 4.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
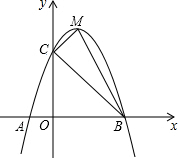 如图,抛物线y=ax2+bx+c交x轴于A(-1,0)、B两点,交y轴于点C(0,5),且过点D(1,8),M为其顶点.
如图,抛物线y=ax2+bx+c交x轴于A(-1,0)、B两点,交y轴于点C(0,5),且过点D(1,8),M为其顶点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com