
【题目】把边长为3的正方形![]() 绕点A顺时针旋转45°得到正方形
绕点A顺时针旋转45°得到正方形![]() ,边
,边![]() 与
与![]() 交于点O,则四边形
交于点O,则四边形![]() 的周长是( )
的周长是( )

A. 6B. ![]() C.
C. ![]() D.
D. ![]()
科目:初中数学 来源: 题型:
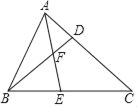
【题目】如图,已知点D、E分别在△ABC的边AC、BC上,线段BD与AE交于点F,且CDCA=CECB.
(1)求证:∠CAE=∠CBD;
(2)若![]() ,求证:ABAD=AFAE.
,求证:ABAD=AFAE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,平行四边形![]() 的顶点
的顶点![]() ,边
,边![]() 落在
落在![]() 正半轴上,
正半轴上,![]() 为线段
为线段![]() 上一点,过点
上一点,过点![]() 分别作
分别作![]() ,
,![]() 交平行四边形各边如图.若反比例函数
交平行四边形各边如图.若反比例函数![]() 的图象经过点
的图象经过点![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,则
,则![]() 的值为__.
的值为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是( )

A. (0,0); B. (0,1); C. (0,2); D. (0,3).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个自然数的立方,可以分裂成若干个连续奇数的和.例如:23,33和43分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即23=3+5;33=7+9+11;43=13+15+17+19;…;若103也按照此规律来进行“分裂”,则103“分裂”出的奇数中,最小的奇数是_________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数![]() 的图象与
的图象与![]() 轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
轴交于A(-3,0),B(1,0)两点,与y轴交于点C.

(1)求这个二次函数的解析式;
(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由;
(3)点Q是直线AC上方的抛物线上一动点,过点Q作QE垂直于![]() 轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】纯电动汽车是指以车载电源为动力,用电机驱动车轮行驶,符合道路交通、安全法规各项要求的车辆.车载电源一般为二次电池,从大的角度讲,纯电动汽车可以摆脱汽车对石油这单一能源的依赖,降低排放染和改善空气质量.从小的角度讲,纯电动车较之普通燃油车最大的优势就是使用成本大幅降低,龙先生欲购买一辆汽车,他比较了两种车的成本请你帮他计算,大约行驶( )公里以上购买燃油汽车划算(精确到个位).
项目 | 电动汽车 | 燃油汽车 |
车价(元) |
|
|
购置税 |
|
|
上牌费 |
|
|
百公里行驶费用(元) |
|
|
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 和函数
和函数![]() 的图象之间的关系,小东根据学习函数的经验,通过画出两个函数图象后,再观察研究.
的图象之间的关系,小东根据学习函数的经验,通过画出两个函数图象后,再观察研究.
下面是小东的探究过程,请补充完成:
(![]() )下表是
)下表是![]() 与
与![]() 的几组对应值.
的几组对应值.
| … |
|
|
|
|
|
|
|
|
|
|
| … |
| … |
|
|
|
|
|
|
|
|
|
|
| … |
下表是![]() 与
与![]() 的几组对应值
的几组对应值
| … |
|
|
|
|
|
|
|
|
|
|
| … |
| … |
|
|
|
|
|
|
|
|
|
|
| … |
请补全表格![]() __________.
__________.
(![]() )如下图,在平面直角坐标系
)如下图,在平面直角坐标系![]() 中,描出了以上表中各对对应值为坐标的点,请根据描出的点,在同一坐标系中画出
中,描出了以上表中各对对应值为坐标的点,请根据描出的点,在同一坐标系中画出![]() 和函数
和函数![]() 的图象.
的图象.

(![]() )观察这两个函数的图象,发现这两个函数图象是关于直线成轴对称的,请画出这条直线.
)观察这两个函数的图象,发现这两个函数图象是关于直线成轴对称的,请画出这条直线.
(![]() )已知
)已知![]() ,借助函数图象比较
,借助函数图象比较![]() ,
, ![]() ,
, ![]() 的大小(用“
的大小(用“![]() ”号连接).
”号连接).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD在平面直角坐标系中的位置如图所示,对角线AC与BD的交点E恰好在y轴上,过点D和BC的中点H的直线交AC于点F,线段DE,CD的长是方程x2﹣9x+18=0的两根,请解答下列问题:
(1)求点D的坐标;
(2)若反比例函数y=![]() (k≠0)的图象经过点H,则k= ;
(k≠0)的图象经过点H,则k= ;
(3)点Q在直线BD上,在直线DH上是否存在点P,使以点F,C,P,Q为顶点的四边形是平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com