
分析 由于3<$\sqrt{10}$<4,由此可确定$\sqrt{10}$的整数部分x=3,接着确定小数部分y=$\sqrt{10}$-3,然后代入所求代数式中恰好利用平方差公式计算出结果.
解答 解:∵3<$\sqrt{10}$<4,
∴$\sqrt{10}$的整数部分x=3,小数部分y=$\sqrt{10}$-3,
∴y(x+$\sqrt{10}$)=($\sqrt{10}$-3)(3+$\sqrt{10}$)=($\sqrt{10}$)2-32=10-9=1.
故答案为:1.
点评 此题考查了二次根式的性质,首先利用二次根式的性质确定x、y的值,然后在代数式中利用平方差公式化简计算即可解决问题.


科目:初中数学 来源: 题型:解答题
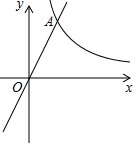 如图,在平面直角坐标系xOy中,反比例函数y=$\frac{8}{x}$的图象与正比例函数y=kx(k≠0)的图象相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0),与y轴交于点C.
如图,在平面直角坐标系xOy中,反比例函数y=$\frac{8}{x}$的图象与正比例函数y=kx(k≠0)的图象相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0),与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AC和BD互相垂直平分 | B. | AB=AD且AC⊥BD | ||
| C. | ∠A=∠B且AC=BD | D. | AB=AD且AC=BD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售时段 | 销售量 | 销售收入 | |
| A型号 | B型号 | ||
| 第一周 | 3台 | 5台 | 1800元 |
| 第二周 | 4台 | 10台 | 3100元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 我区某校数学学习小组利用所学的三角函数知识测量我区某座山的高度.如图,他们在山脚下的B处测得山顶C的仰角是45°,从B处沿坡度为1:$\sqrt{3}$的斜坡前进100米到达山腰的一个观景点D,在点D处再次测得山顶C的仰角为60°,则该座山的高度AC为( )(注:结果精确到1米,参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
我区某校数学学习小组利用所学的三角函数知识测量我区某座山的高度.如图,他们在山脚下的B处测得山顶C的仰角是45°,从B处沿坡度为1:$\sqrt{3}$的斜坡前进100米到达山腰的一个观景点D,在点D处再次测得山顶C的仰角为60°,则该座山的高度AC为( )(注:结果精确到1米,参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)| A. | 86米 | B. | 87米 | C. | 136米 | D. | 137米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
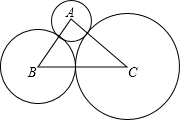 如图,⊙A、⊙B、⊙C两两外切,AB=10,BC=21,sinB=$\frac{4}{5}$.
如图,⊙A、⊙B、⊙C两两外切,AB=10,BC=21,sinB=$\frac{4}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com