
【题目】如图,已知关于![]() 的一元二次函数
的一元二次函数![]() (
(![]() )的图象与
)的图象与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,顶点为
,顶点为![]() .
.

⑴ 求出一元二次函数的关系式;
⑵ 点![]() 为线段
为线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,垂足为
,垂足为![]() .若
.若![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
⑶ 探索线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 为直角三角形,如果存在,求出
为直角三角形,如果存在,求出![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() (
(![]() );(3)P点坐标为:
);(3)P点坐标为:![]() ,
,![]() .
.
【解析】
(1)可根据OB、OC的长得出B、C两点的坐标,然后用待定系数法即可求出抛物线的解析式.
(2)求出P点的坐标,据此可根据三角形的面积计算方法求出S与m的函数关系式.
(3)先根据抛物线的解析式求出M的坐标,进而可得出直线BM的解析式,以及P点纵坐标,即可得出符合条件的P点的坐标.
解:⑴![]() 、
、![]() .
.
![]()
解得![]() ,
,
所以![]()
⑵∵y=-x2+2x+3=-(x-1)2+4,
∴![]() .
.
设![]() :
:![]() ,
,
则![]() 得
得![]() 所以
所以![]() .
.
所以![]() ,
,
![]() (
(![]() )
)
(3)∵若∠PDC是直角,则点C在x轴上,由函数图象可知点C在y轴的正半轴上,

∴∠PDC≠90°,
在△PCD中,当∠DPC=90°时,
当CP∥AB时,
∵PD⊥AB,
∴CP⊥PD,
∴PD=OC=3,
∴P点纵坐标为:3,代入y=-2x+6,
![]() ,此时P
,此时P![]() ,
,
当∠P′CD′=90°时,△COD′∽△D′CP′,
此时CD′2=COP′D′,
即9+m2=3(-2m+6),
∴m2+6m-9=0,
解得:![]() ,
,
∵1≤m<3,
![]() ,
,
![]() ,
,
综上所述:P点坐标为:![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,甲、乙两人在玩转盘游戏时,准备了两个可以自由转动的转盘A,B,每个转盘被分成面积相等的几个扇形,并在每一个扇形内标上数字.游戏规则:同时转动两个转盘,当转盘停止后,指针所指区域的数字之和为0时,甲获胜;数字之和为1时,乙获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向某一区域为止.

(1)用画树状图或列表法求乙获胜的概率;
(2)这个游戏规则对甲、乙双方公平吗?请判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解全校![]() 名同学对学校设置的体操、篮球、足球、跑步、舞蹈等课外活动项目的喜爱情况,在全校范围内随机抽取了若干名同学,对他们喜爱的项目(每人选一项)进行了问卷调查,将数据进行了统计,并绘制成了如图所示的条形统计图和扇形统计图(均不完整),请回答下列问题.
名同学对学校设置的体操、篮球、足球、跑步、舞蹈等课外活动项目的喜爱情况,在全校范围内随机抽取了若干名同学,对他们喜爱的项目(每人选一项)进行了问卷调查,将数据进行了统计,并绘制成了如图所示的条形统计图和扇形统计图(均不完整),请回答下列问题.
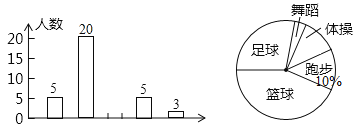
(1)在这次问卷调查中,共抽查了_________名同学;
(2)补全条形统计图;
(3)估计该校![]() 名同学中喜爱足球活动的人数;
名同学中喜爱足球活动的人数;
(4)在体操社团活动中,由于甲、乙、丙、丁四人平时的表现优秀,现决定从这四人中任选两名参加体操大赛.用树状图或列表法求恰好选中甲、乙两位同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,
,![]() ,点
,点![]() 的坐标是
的坐标是![]() .
.
(1)如图1,求直线![]() 的解析式;
的解析式;
(2)如图2,点![]() 在第一象限内,连接
在第一象限内,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的而积为S,求S与
的而积为S,求S与![]() 的函数关系式(不要求写出自变量
的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
(3)如图3,在(2)的条件下,过点![]() 作
作![]() 轴,连接
轴,连接![]() 、
、![]() ,若
,若![]() ,
,![]() 时,求
时,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
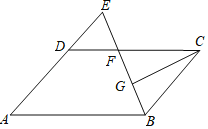
【题目】如图,在平行四边形ABCD中,AB=12,AD=8,∠ABC的平分线交CD于点F,交AD的延长线于点E,CG⊥BE,垂足为G,若EF=2,则线段CG的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推进“传统文化进校园”活动,某校准备成立“经典诵读”、“传统礼仪”、“民族器乐”和“地方戏曲”等四个课外活动小组.学生报名情况如图(每人只能选择一个小组):
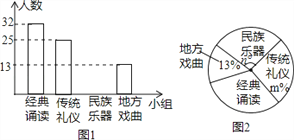
(1)报名参加课外活动小组的学生共有 人,将条形图补充完整;
(2)扇形图中m= ,n= ;
(3)根据报名情况,学校决定从报名“经典诵读”小组的甲、乙、丙、丁四人中随机安排两人到“地方戏曲”小组,甲、乙恰好都被安排到“地方戏曲”小组的概率是多少?请用列表或画树状图的方法说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西南大学附中一年一度的“缤纷节”受到社会各界的高度赞扬,2018年12月14日西南大学附中成功举办了第十八届缤纷节,为成功筹办此次缤纷节,学校后勤工作人员进行了繁琐细致地准备工作,为了搭建舞台、后勤服务平台和安排全校师生及家长朋友们的座位,学校需要购买钢材1380根,购买胶板凳2300个.现安排A,B两种型号的货车共10辆运往学校,已知一辆A型货车可以用150根钢材和200个板凳装满,一辆B型货车可以用120根钢材和350个板凳装满,并且一辆A型货车的运费为500元,一辆B型货车的运费为520元;设运输钢材和板凳的总费用为y元,租用A型货车x辆.
(1)试写出y与x之间的函数关系式,并写出x的取值范围;
(2)按要求有哪几种运输方案,运费最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(a,0),B(0,b),且a,b满足a2-2ab+b2+(b-4)2=0,点C为线段AB上一点,连接OC.
(1)直接写出a=____,b=_____;
(2)如图1,P为OC上一点,连接PA,PB.若PA=B0,∠BPC=30°.求点P的纵坐标;
(3)如图2,在(2)的条件下,点M是AB上一动点,以OM为边在OM的右侧作等边△OMN,连接CN.若OC=t,求ON+CN的最小值(结果用含t的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为奖励在学校体育艺术节中表现突出的25名同学,派李老师为这些同学购买奖品,要求每人一件.李老师到文具店看了商品后,决定奖品在钢笔和笔记本中选择.如果买4个笔记本和2支钢笔,则需86元;如果买3个笔记本和1支钢笔,则需57元.
(1)求笔记本和钢笔的单价分别为多少元?
(2)售货员提示,购买笔记本没有优惠;买钢笔有优惠,具体方法是:如果买钢笔超过10支,那么超出部分可以享受8折优惠,若买x(x>10)支钢笔,所需总费用为y元,请你求出y与x之间的函数关系式;
(3)在(2)的条件下,如果买同一种奖品,请你帮忙计算说明,买哪种奖品费用更低.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com