
【题目】如图,某校初一(2)班组织学生从A地到B地步行野营,匀速前进,该班师生共56人,每8人排成一排,相邻两排之间间隔1米,途中经过一座桥CD,队伍从开始上桥到刚好完全离开桥共用了150秒,当队尾刚好走到桥的一端D处时,排在队尾的游班长发现小蒋还在桥的另一端C处拍照,于是以队伍1.5倍的速度返回去找小萍,同时队伍仍按原速度继续前行,30秒后,小蒋发现游班长返回来找他,便立刻以2.1米/秒的速度向游班长方向行进,小蒋行进40秒后与游班长相遇,相遇后两人以队伍2倍的速度前行追赶队伍.
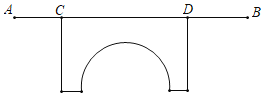
(1)初一(2)班的队伍长度为 米;
(2)求班级队伍行进的速度(列一元一次方程解决问题);
(3)请问:游班长从D处返回赵小萍开始到他们两人追上队首的刘老师一共用了多少时间?
【答案】(1)6秒;(2)2米/秒;(3)248秒.
【解析】
(1)由题意得56÷8=7(排),则队伍长度为(7-1)×1=6(米);
(2)设队伍行进的速度为x米/秒,由路程=桥长+队伍长,列出方程,解方程即可;
(3)设小蒋与游班长相遇后两人追上队首的刘老师用了y小时,根据追队伍的路程-队伍走的路程=他们与队伍的距离,列出方程,解方程即可.
解:(1)由题意得56÷8=7(排),
由相邻两排之间间隔1米,则队伍长度为(7-1)×1=6(米);
故答案为:6;
(2)设班级队伍行进的速度为x米/秒,由题意得:
150x=1.5x(30+40)+2.1×40+6,
解得:x=2,
所以班级队伍行进的速度为2米/秒;
(3)设相遇后追上刘老师用时y小时,小蒋与游班长的追赶速度为4米/秒,他们与队首的刘老师的距离为1.5×2×70+2×70+6=356(米)
由题意得:4y-2y=356,
解得:y=178
70+178=248秒
所以答案班长从D处返回找小蒋开始到他们两人追上队首的刘老师一共用了248秒


科目:初中数学 来源: 题型:
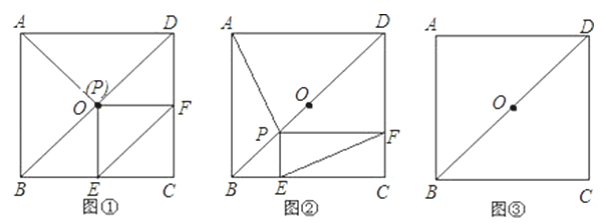
【题目】正方形ABCD中,点O是对角线DB的中点,点P是DB所在直线上的一个动点,PE⊥BC于E,PF⊥DC于F.
(1)当点P与点O重合时(如图①),猜测AP与EF的数量及位置关系,并证明你的结论;
(2)当点P在线段DB上(不与点D、O、B重合)时(如图②),探究(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由;
(3)当点P在DB的长延长线上时,请将图③补充完整,并判断(1)中的结论是否成立?若成立,直接写出结论;若不成立,请写出相应的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,锐角△ABC内接于⊙O,若⊙O的半径为6,sinA=![]() ,求BC的长.
,求BC的长.

【答案】BC=8.
【解析】试题分析:通过作辅助线构成直角三角形,再利用三角函数知识进行求解.
试题解析:作⊙O的直径CD,连接BD,则CD=2×6=12.
∵![]()
∴![]()
∴![]()

点睛:直径所对的圆周角是直角.
【题型】解答题
【结束】
22
【题目】如图,一次函数y=k1x+b与反比例函数y=![]() 的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式k1x+b>![]() 的解集;
的解集;
(3)若P(p,y1),Q(﹣2,y2)是函数y=![]() 图象上的两点,且y1≥y2,求实数p的取值范围.
图象上的两点,且y1≥y2,求实数p的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邮递员骑车从邮局出发,先向西骑行 2 km 到达 A 村,继续向西骑行 3 km 到达 B 村, 然后向东骑行 9 km 到达 C 村,最后回到邮局.
(1)以邮局为原点,以向东方向为正方向,用 1 cm 表示 1 km 画数轴,并在该数轴上表示 A,B,C 三个村庄的位置;
(2)C 村离 A 村有多远?
(3)邮递员一共骑行了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一个点从数轴上的原点开始,先向右移动2个单位长度,再向左移动5个单位长度,可以看到终点表示是-3,已知A、B是数轴上的点,请参照下图并思考,完成下列各题.
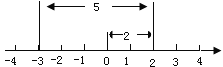
(1)如果点A表示的数-1,将点A向右移动4个单位长度,那么终点B表示的数是____.A、B两点间的距离是__________.
(2)如果点A表示的数2,将点A向左移动6个单位长度,再向右移动3个单位长度,那么终点B表示的数是____.A、B两点间的距离是____.
(3)如果点A表示的数m,将点A向左移动n个单位长度,再向左移动p个单位长度,那么请你猜想终点B表示的数是___.A、B两点间的距离是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上,点O为原点,点A对应的数为11,点B对应的数为b,点C在点B右侧,长度为3个单位的线段BC在数轴上移动,
(1)如图1,当线段BC在O,A两点之间移动到某一位置时,恰好满足线段AC=OB,求此时b的值;
(2)线段BC在数轴上沿射线AO方向移动的过程中,是否存在AC﹣OB=![]() AB?若存在,求此时满足条件的b的值;若不存在,说明理由.
AB?若存在,求此时满足条件的b的值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的知识竞赛活动中,老师将八年级一班和二班全部学生的成绩整理并绘制成如下统计表:
得分(分) 人数(人) 班级 | 50 | 60 | 70 | 80 | 90 | 100 |
一班 | 2 | 5 | 10 | 13 | 14 | 6 |
二班 | 4 | 4 | 16 | 2 | 12 | 12 |
(1)现已知一班和二班的平均分相同,请求出其平均分.
(2)请分别求出这两班的中位数和众数,并进一步分析这两个班级在这次竞赛中成绩的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
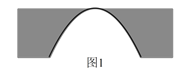
【题目】河上有一座桥孔为抛物线形的拱桥(如图 ![]() ),水面宽
),水面宽 ![]() 时,水面离桥孔顶部
时,水面离桥孔顶部 ![]() ,因降暴雨水面上升
,因降暴雨水面上升 ![]() .
.
(1)建立适当的坐标系,并求暴雨后水面的宽;(结果保留根号)
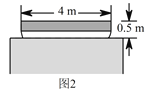
(2)一艘装满物资的小船,露出水面的部分高为 ![]() ,宽
,宽 ![]() (横断面如图
(横断面如图 ![]() 所示),暴雨后这艘船能从这座拱桥下通过吗?
所示),暴雨后这艘船能从这座拱桥下通过吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
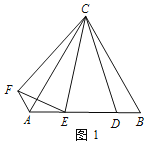
【题目】【操作发现】如图 1,△ABC 为等边三角形,点 D 为 AB 边上的一点,∠DCE=30°,将线段 CD 绕点 C 顺时针旋转 60°得到线段 CF,连接 AF、EF. 请直接 写出下列结果:
① ∠EAF的度数为__________;
② DE与EF之间的数量关系为__________;
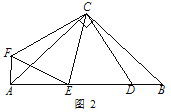
【类比探究】如图 2,△ABC 为等腰直角三角形,∠ACB=90°,点 D 为 AB 边上的一点∠DCE=45°,将线段 CD 绕点 C 顺时针旋转 90°得到线段 CF,连接 AF、EF.
①则∠EAF的度数为__________;
② 线段 AE,ED,DB 之间有什么数量关系?请说明理由;
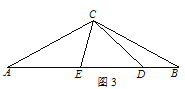
【实际应用】如图 3,△ABC 是一个三角形的余料.小张同学量得∠ACB=120°,AC=BC, 他在边 BC 上取了 D、E 两点,并量得∠BCD=15°、∠DCE=60°,这样 CD、CE 将△
ABC 分成三个小三角形,请求△BCD、△DCE、△ACE 这三个三角形的面积之比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com