
【题目】一辆轿车从甲地出发开往乙地,同时,一辆客车从乙地开往甲地,一开始两车的速度相同,出发半小时后,客车因出现故障维修了一段时间,修好后为了不耽误乘客的时间,客车加快速度前进,结果与轿车同时到达各自的目的地.设轿车出发th后,与客车的距离为Skm,图中的折线(A→B→C→D→E)表示S与t之间的函数关系.

(1)甲、乙两地相距 km,轿车的速度为 km/h;
(2)求m与n的值;
(3)求客车修好后行驶的速度;
(4)求线段DE所对应的函数关系式,并注明自变量的取值范围.
【答案】(1)120,60;(2)m=60,n=0.8;(3)客车修好后行驶的速度为75(千米/时).
(4)线段DE所对应的函数关系式为S=135t﹣150(![]() ≤t≤2).
≤t≤2).
【解析】
试题分析:(1)结合函数图象,可知当t=0时,S的值即为甲、乙两地之间的距离,再由“速度=路程÷时间”即可得出轿车的速度;
(2)根据B点的横坐标结合“两车间减少的距离=两车速度和×行驶时间”即可得出m的值,再由B、C两点间的纵坐标,利用“时间=纵坐标之差÷轿车的速度”可得出点B、C横坐标之差,再加上0.5即可得出n的值;
(3)由(2)可知客车修车耽误的时间,根据客车原来的速度可算出该时间段应该行驶的路程,将这段距离平摊到剩下的1.2小时中再加上原来的速度,即可得出客车修好后的速度;
(4)利用“时间=路程÷两车速度和”得出点C、D横坐标之差,结合点C的横坐标即可得出点D的坐标,设线段DE所对应的函数关系式为S=kt+b,根据点D、E的坐标利用待定系数法即可得出结论.
试题解析:(1)当t=0时,S=120,
故甲、乙两地相距为120千米;
轿车的速度为:120÷2=60(千米/时).
故答案为:120;60.
(2)当t=0.5时,m=120﹣(60+60)×0.5=60.
在BC段只有轿车在行驶,
∴n=0.5+(60﹣42)÷60=0.8.
故m=60,n=0.8.
(3)客车维修的时间为:0.8﹣0.5=0.3(小时),
客车修好后行驶的速度为:0.3×60÷(2﹣0.8)+60=75(千米/时).
(4)∵42÷(60+75)=![]() ,
,
∴点D的横坐标为:0.8+![]() =
=![]() ,
,
即点D的坐标为(![]() ,0).
,0).
设线段DE所对应的函数关系式为S=kt+b,
将点D(![]() ,0)、点E(2,120)代入函数解析式得:
,0)、点E(2,120)代入函数解析式得:
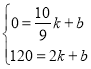 ,解得
,解得![]() .
.
∴线段DE所对应的函数关系式为S=135t﹣150(![]() ≤t≤2).
≤t≤2).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,一架2.5米长的梯子,斜靠在一竖直的墙上,这时梯足到墙底端的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么梯足将向外移多少米?(5分)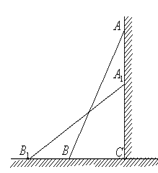
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
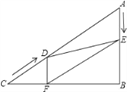
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,AB=10,AC=8,点Q在AB上,且AQ=2,过Q做QR⊥AB,垂足为Q,QR交折线AC﹣CB于R(如图1),当点Q以每秒2个单位向终点B移动时,点P同时从A出发,以每秒6个单位的速度沿AB﹣BC﹣CA移动,设移动时间为t秒(如图2).
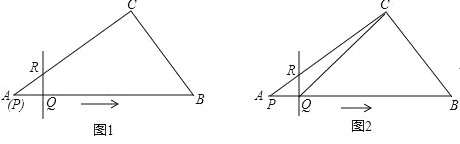
(1)求△BCQ的面积S与t的函数关系式.
(2)t为何值时,QP∥AC?
(3)t为何值时,直线QR经过点P?
(4)当点P在AB上运动时,以PQ为边在AB上方所作的正方形PQMN在Rt△ABC内部,求此时t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
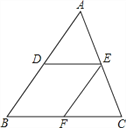
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBFE是菱形?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com