
| A. | $\overrightarrow{a}$∥$\overrightarrow{c}$,$\overrightarrow{b}$∥$\overrightarrow{c}$ | B. | $\overrightarrow{a}$=3$\overrightarrow{c}$,$\overrightarrow{b}$=-$\overrightarrow{c}$ | C. | $\overrightarrow{a}$=-5$\overrightarrow{b}$ | D. | $|{\overrightarrow a}|=2|{\overrightarrow b}|$ |
分析 根据向量的性质进行逐一判定即可.
解答 解:A、由于$\overrightarrow{a}$∥$\overrightarrow{c}$,所以$\overrightarrow{a}$与$\overrightarrow{c}$的方向相同,由于$\overrightarrow{b}$∥$\overrightarrow{c}$,所以$\overrightarrow{b}$与$\overrightarrow{c}$的方向相同,所以$\overrightarrow{a}$∥$\overrightarrow{b}$,故本选项不符合题意;
B、因为$\overrightarrow{a}$=3$\overrightarrow{c}$,所以$\overrightarrow{a}$与3$\overrightarrow{c}$的方向相同,由于$\overrightarrow{b}$=-$\overrightarrow{c}$,所以$\overrightarrow{b}$与$\overrightarrow{c}$的方向相反,所以$\overrightarrow{a}$∥$\overrightarrow{b}$,故本选项不符合题意;
C、因为$\overrightarrow{a}$=-5$\overrightarrow{b}$,所以$\overrightarrow{a}$与$\overrightarrow{b}$的方向相反,所以$\overrightarrow{a}$∥$\overrightarrow{b}$,故本选项不符合题意;
D、因为|$\overrightarrow{a}$|=2|$\overrightarrow{b}$|,所以$\overrightarrow{a}$与$\overrightarrow{b}$的方向不能确定,故不能判定其位置关系,故本选项符合题意.
故选D.
点评 本题考查的是向量中平行向量的定义,即方向相同或相反的非零向量a、b叫做平行向量.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,DE⊥AB于E,且AE=6cm,则△ABC的周长为( )
如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,DE⊥AB于E,且AE=6cm,则△ABC的周长为( )| A. | 24cm | B. | (12+6$\sqrt{2}$)cm | C. | 10cm | D. | (8+6$\sqrt{3}$)cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
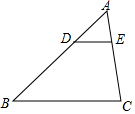 如图,在△ABC中,点D、E分别在AB、AC上,且DE∥BC,那么下列说法中错误的是( )
如图,在△ABC中,点D、E分别在AB、AC上,且DE∥BC,那么下列说法中错误的是( )| A. | $\frac{AD}{BD}$=$\frac{AE}{EC}$ | B. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | C. | $\frac{DE}{BC}$=$\frac{AD}{DB}$ | D. | $\frac{DE}{BC}$=$\frac{AE}{AC}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
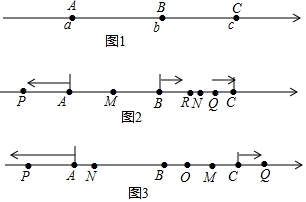 如图,已知数轴上有三点A、B、C,它们对应的数分别为a,b,c,且c-b=b-a,点C对应的数是20.
如图,已知数轴上有三点A、B、C,它们对应的数分别为a,b,c,且c-b=b-a,点C对应的数是20.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com