练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．已知△ABC的周长是l，BC=l-2AB，则下列直线一定为△ABC的对称轴的是（　　）
    A．△ABC的边AB的垂直平分线B．∠ACB的平分线所在的直线
    C．△ABC的边BC上的中线所在的直线D．△ABC的边AC上的高所在的直线

    分析 根据条件可以推出AB=AC，由此即可判断．

    解答 解：∵l=AB+BC+AC，
    ∴BC=l-2AB=AB+BC+AC-2AB，
    ∴AB=AC，
    ∴△ABC中BC边中线所在的直线是△ABC的对称轴，
    故选C．

    点评 本题考查对称轴、三角形周长、等腰三角形的性质等知识，解题的关键是根据条件推出AB=AC，属于中考常考题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    11．计算：|-4|-$\sqrt{9}$=1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．函数y=$\frac{1}{\sqrt{x-2}}$有意义，则实数x的取值范围是x＞2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

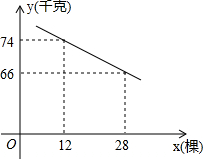    9．某片果园有果树80棵，现准备多种一些果树提高果园产量，但是如果多种树，那么树之间的距离和每棵树所受光照就会减少，单棵树的产量随之降低．若该果园每棵果树产果y（千克），增种果树x（棵），它们之间的函数关系如图所示．
    （1）求y与x之间的函数关系式；
    （2）在投入成本最低的情况下，增种果树多少棵时，果园可以收获果实6750千克？
    （3）当增种果树多少棵时，果园的总产量w（千克）最大？最大产量是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．在平面直角坐标系内按下列要求完成作图（不要求写作法，保留作图痕迹）．
    （1）以（0，0）为圆心，3为半径画圆；
    （2）以（0，-1）为圆心，1为半径向下画半圆；
    （3）分别以（-1，1），（1，1）为圆心，0.5为半径画圆；
    （4）分别以（-1，1），（1，1）为圆心，1为半径向上画半圆．
    （向上、向下指在经过圆心的水平线的上方和下方）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．公元3世纪，我国古代数学家刘徽就能利用近似公式$\sqrt{{a^2}+r}≈a+\frac{r}{2a}$得到的近似值．他的算法是：先将$\sqrt{2}$看出$\sqrt{{1^2}+1}$：由近似公式得到$\sqrt{2}≈1+\frac{1}{2×1}=\frac{3}{2}$；再将$\sqrt{2}$看成$\sqrt{{{（{\frac{3}{2}}）}^2}+（{-\frac{1}{4}}）}$，由近似值公式得到$\sqrt{2}≈\frac{3}{2}+\frac{{-\frac{1}{4}}}{{2×\frac{3}{2}}}=\frac{17}{12}$；…依此算法，所得$\sqrt{2}$的近似值会越来越精确．当$\sqrt{2}$取得近似值$\frac{577}{408}$时，近似公式中的a是$\frac{17}{12}$或$\frac{24}{17}$，r是-$\frac{1}{144}$或$\frac{2}{289}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

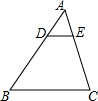    13．如图，在△ABC中，DE∥BC，$\frac{AD}{AB}$=$\frac{1}{3}$，BC=12，则DE的长是（　　）
    A．3B．4C．5D．6

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，在平行四边形ABCD中，以点A为圆心，AB长为半径画弧交AD于点F，再分别以点B、F为圆心，大于$\frac{1}{2}BF$长为半径画弧，两弧交于一点P，连
    接AP并延长交BC于点E，连接EF． 
    （1）四边形ABEF是菱形；（选填矩形、菱形、正方形、无法确定）（直接填写结果）
    （2）AE，BF相交于点O，若四边形ABEF的周长为40，BF=10，则AE的长为10$\sqrt{3}$，∠ABC=120°．（直接填写结果）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．若$\sqrt{2016}$≈44.90，$\sqrt{201.6}$≈14.20，则$\sqrt{20.16}$≈4.490．

    查看答案和解析>>

    同步练习册答案