
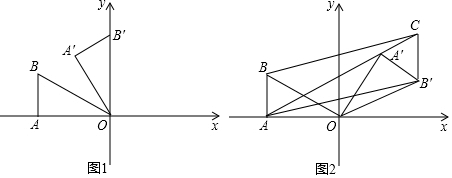
���� ������ͼ1�У���A��E��OB����E����ֱ�����������EO��A��E���ɽ�����⣻
������ͼ2�У����ۣ��ı���AB��CB��ƽ���ı��Σ�ֻҪ֤��B��C��AB��B��C=AB��
�ڹ���A����A��E��x����E������B����B��F��A��E��F����ֱ�����������OE��EF��B��F���ɣ�
����B��Cɨ�������=Sƽ���ı���B��B��C��C�����ɴ˼��㼴�ɣ�
��� �⣺������ͼ1�У���A��E��OB����E��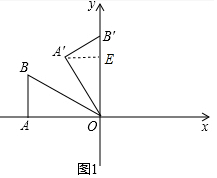
��Rt���OA��B���У��ߡ�A��OB��=30�㣬OA��=2$\sqrt{3}$��
��cos30��=$\frac{OA��}{OB��}$��
��OB��=4��
��B�䣨0��4����
��Rt��OA��E����OA��=2$\sqrt{3}$��
��A��E=$\sqrt{3}$��OE=$\sqrt{3}$A��E=3��
��A�䣨-$\sqrt{3}$��3����
�ʴ�Ϊ��-$\sqrt{3}$��3������0��4����
������ͼ2�У����ۣ��ı���AB��CB��ƽ���ı��Σ�
���ɣ���B��C��AB��
���B��CA=��BAC��
�ߡ�BAC+��CAO=90�㣬
���B��CA��+��CAO=90�㣬
�֡ߡ�B��A��C+��OA��A=90�㣬����ת�õ�OA=OA�䣬���CAO=��OA��A��
���B��CA��=��B��A��C��
��B��C=B��A�䣬
�֡�A��B��=AB��
��B��C=AB��
���ı���AB��CB��ƽ���ı��Σ�
�ڹ���A����A��E��x����E��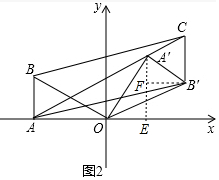
��A��-2$\sqrt{3}$��0�����ɵ�OA=2$\sqrt{3}$��
�֡ߡ�OAB=90�㣬��AOB=30�㣬
��AB=2��OB=4����OA��=2$\sqrt{3}$��A��B��=2��
�ɡ�AOA��=135�㣬�õ���A��OE=45�㣬
��OE=A��E=$\frac{\sqrt{2}}{2}$OA��=$\sqrt{6}$��
���A�䣨$\sqrt{6}$��$\sqrt{6}$����
����B����B��F��A��E��F��
�ɡ�EA��O=45�㣬�á�EA��B��=45�㣬
��B��F=A��F=$\frac{\sqrt{2}}{2}$��2=$\sqrt{2}$��
��EF=$\sqrt{6}$-$\sqrt{2}$��OE+B��F=$\sqrt{6}$+$\sqrt{2}$��
���B�䣨$\sqrt{6}$+$\sqrt{2}$��$\sqrt{6}$-$\sqrt{2}$����
������ͼ3�У�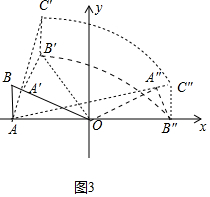
B��Cɨ�������=Sƽ���ı���B��B��C��C��=6��2=12��
���� ���⿼���������ۺ��⡢��ת�任����ֱ�������Ρ�������Ǻ�����ƽ���ı��ε����ʵ�֪ʶ������Ĺؼ���ѧ�����ӳ��ø����ߣ�����ֱ�������ν�����⣬�����п�ѹ���⣮


 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ABΪ��O��ֱ������P�ǡ�O��һ�㣬PD���O�����ڵ�C����BA���ӳ��߽��ڵ�D��DE��PO����PO���ӳ����ڵ�E������PB����EDB=��EPB��
��ͼ��ABΪ��O��ֱ������P�ǡ�O��һ�㣬PD���O�����ڵ�C����BA���ӳ��߽��ڵ�D��DE��PO����PO���ӳ����ڵ�E������PB����EDB=��EPB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{3}$ | B�� | $\frac{1}{4}$ | C�� | $\frac{1}{6}$ | D�� | $\frac{1}{9}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
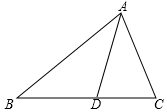 ʵ������
ʵ�������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ������С����Ҫ����һ��ѧ����ͼ����6000�ף�Ϊ�˿����˼ס��������ľӹ�������֪�׳��ļӹ��������ҳ���1.5�����Ҽ׳������ӹ�������ͼ��������Ҫ���������ҳ������ӹ�������ͼ��������Ҫ��������10�죬���˽���ֻ�ͼ���ߣ��׳��ij����۸�Ϊ6Ԫ/�ף��ҳ��ij����۸�Ϊ5.6Ԫ/�ף�
������С����Ҫ����һ��ѧ����ͼ����6000�ף�Ϊ�˿����˼ס��������ľӹ�������֪�׳��ļӹ��������ҳ���1.5�����Ҽ׳������ӹ�������ͼ��������Ҫ���������ҳ������ӹ�������ͼ��������Ҫ��������10�죬���˽���ֻ�ͼ���ߣ��׳��ij����۸�Ϊ6Ԫ/�ף��ҳ��ij����۸�Ϊ5.6Ԫ/�ף��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
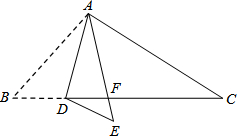 ��ͼ���ڡ�ABC�У���D��BC���ϵ�һ�㣬��B=50�㣬��BAD=30�㣬����ABD��AD�۵��õ���AED��AE��BC���ڵ�F��
��ͼ���ڡ�ABC�У���D��BC���ϵ�һ�㣬��B=50�㣬��BAD=30�㣬����ABD��AD�۵��õ���AED��AE��BC���ڵ�F���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com