
【题目】小红同学要测量![]() ,
,![]() 两地的距离,但
两地的距离,但![]() ,
,![]() 之间有一水池,不能直接测量,于是她在
之间有一水池,不能直接测量,于是她在![]() ,
,![]() 同一水平面上选取了一点
同一水平面上选取了一点![]() ,点
,点![]() 可直接到达
可直接到达![]() ,
,![]() 两地.她测量得到
两地.她测量得到![]() 米,
米,![]() 米,
米,![]() .请你帮助小红同学求出
.请你帮助小红同学求出![]() ,
,![]() 两点之间的距离.
两点之间的距离.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AD⊥BC,EG⊥BC,垂足分别为D、G、AD平分∠BAC,求证:∠E=∠4.
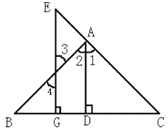
证明:∵AD⊥BC,EG⊥BC(已知)
∴AD∥EG( )
∴∠2=∠3( )
∠1= (两直线平行,同位角相等)
∵AD平分∠BAC(已知)
∴∠1=∠2( )
∴∠E=∠3( )
∵∠3=∠4( )
∴∠E=∠4(等量代换)
查看答案和解析>>
科目:初中数学 来源: 题型:
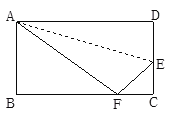
【题目】如图,小莹用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,BC长为10cm.当小莹折叠时,顶点D落在BC边上的点F处(折痕为AE).则此时EC=( )cm
A.4B.![]() C.
C.![]() D.3
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某饮料经营部每天的固定成本为200元,其销售的饮料每瓶进价为5元.销售单价与日平均销售的关系如下:
销售单价(元) | 6 | 6.5 | 7 | 7.5 | 8 | 8.5 | 9 |
日平均销售量(瓶) | 480 | 460 | 440 | 420 | 400 | 380 | 360 |
(1)若记销售单价比每瓶进价多x元,则销售量为_____(用含x的代数式表示);
求日均毛利润(日均毛利润=(每瓶售价-每瓶进价)×日均销售量-固定成本)y与x之间的函数关系式.
(2)若要使日均毛利润达到1400元,则销售单价应定为多少元?
(3)若要使日均毛利润达到最大,销售单价应定为多少元?最大日均毛利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为![]() ,C点的坐标为
,C点的坐标为![]() ,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着
,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着![]() 的路线移动
的路线移动![]() 即:沿着长方形移动一周
即:沿着长方形移动一周![]() .
.
![]() 写出点B的坐标
写出点B的坐标![]() ______
______![]()
![]() 当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
![]() 在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一次函数![]() ,下列结论正确的是( )
,下列结论正确的是( )
A.函数值随自变量的增大而增大
B.函数的图象不经过第一象限
C.函数的图象向下平移4个单位长度得![]() 的图象
的图象
D.函数的图象与![]() 轴的交点坐标是
轴的交点坐标是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,A(a,0)是x轴正半轴上一点,C是第四象限一点,CB⊥y轴,交y轴负半轴于B(0,b),且(a-3)2+|b+4|=0,S四边形AOBC=16.
(1)求C点坐标;
(2)如图2,设D为线段OB上一动点,当AD⊥AC时,∠ODA的角平分线与∠CAE的角平分线的反向延长线交于点P,求∠APD的度数.
(3)如图3,当D点在线段OB上运动时,作DM⊥AD交BC于M点,∠BMD、∠DAO的平分线交于N点,则D点在运动过程中,∠N的大小是否变化?若不变,求出其值,若变化,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点 A(﹣2,0),B(2,0),C(0,2),点 D,点E分别是 AC,BC的中点,将△CDE绕点C逆时针旋转得到△CD′E′,及旋转角为α,连接 AD′,BE′.
(1)如图①,若 0°<α<90°,当 AD′∥CE′时,求α的大小;
(2)如图②,若 90°<α<180°,当点 D′落在线段 BE′上时,求 sin∠CBE′的值;
(3)若直线AD′与直线BE′相交于点P,求点P的横坐标m的取值范围(直接写出结果即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,在平面直角坐标系中,O为原点,平行四边形ABCD的边BC在x轴上,D点在y轴上,C点坐标为(2,0),BC=6,∠BCD=60°,点E是AB上一点,AE=3EB,⊙P过D,O,C三点,抛物线![]() 过点D,B,C三点.
过点D,B,C三点.

(1)求抛物线的解析式;
(2)求证:ED是⊙P的切线;
(3)若将△ADE绕点D逆时针旋转90°,E点的对应点E′会落在抛物线![]() 上吗?请说明理由;
上吗?请说明理由;
(4)若点M为此抛物线的顶点,平面上是否存在点N,使得以点B,D,M,N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com