
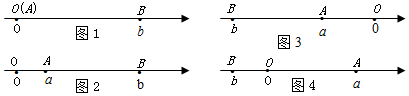
分析 (2)①根据两点之间的距离公式即可求解;
②在数轴上,某点到-1所对应的点的距离为2;
③利用数轴解决:把|x+1|+|x-2|=3理解为:在数轴上,某点到-1所对应的点的距离和到2所对应的点的距离之和为3,然后根据数轴可写出满足条件的整数即可.
解答 解:(2)①数轴上表示2和5的两点之间的距离是5-2=3;
数轴上表示-2和-5的两点之间的距离是-2-(-5)=3;
数轴上表示1和-3的两点之间的距离是|1-(-3)|=4;
②数轴上表示x和-1的两点A和B之间的距离是|x-(-1)|=|x+1|,
|AB|=2,可理解为:在数轴上,某点到-1所对应的点的距离为2,则x=-3或1;
故答案是:7或-4;
③式子|x+1|+|x-2|=3可理解为:在数轴上,某点到-1所对应的点的距离和到2所对应的点的距离之和为3,
所以满足条件的整数可为-1,0,1,2.
故答案是:3,3,4;|x+1|,-3或1;-1,0,1,2.
点评 此题主要考查了去绝对值和数轴相联系的综合试题以及去绝对值的方法和去绝对值在数轴上的运用,难度较大,去绝对的关键是确定绝对值里面的数的正负性.


科目:初中数学 来源: 题型:选择题
| A. | (x+2)2=4 | B. | (x-2)2=4 | C. | (x-2)2=8 | D. | (x+2)2=8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com