
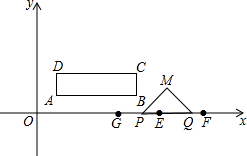
 ��ͼ�����ε��ĸ�����ΪA��1��1����B��5��1����C��5��2����D��1��2������E��F������ֱ�Ϊ��6��0������8��0��������P�ӵ�E��������ÿ��2����λ���ȵ��ٶ���EO�����˶��������O��������ԭ�����ٶ���OE���أ���һ����Q�ӵ�F��������ÿ��1����λ���ȵ��ٶ���FO�����˶�����P��Qͬʱ��������������ʱֹͣ�˶����ڵ�P��Q���˶������У���PQΪб����x���Ϸ�������ֱ��������PQM�����˶�ʱ��Ϊt��
��ͼ�����ε��ĸ�����ΪA��1��1����B��5��1����C��5��2����D��1��2������E��F������ֱ�Ϊ��6��0������8��0��������P�ӵ�E��������ÿ��2����λ���ȵ��ٶ���EO�����˶��������O��������ԭ�����ٶ���OE���أ���һ����Q�ӵ�F��������ÿ��1����λ���ȵ��ٶ���FO�����˶�����P��Qͬʱ��������������ʱֹͣ�˶����ڵ�P��Q���˶������У���PQΪб����x���Ϸ�������ֱ��������PQM�����˶�ʱ��Ϊt������ ��1�������P�˶���·�̼��ɽ�����⣮
��2������P�ӵ�E�˶���Oʱ����M���������߶�AB�ϣ�����P�ӵ�O���E�˶�ʱ����M���߶�AB��ʱ��·�̷��̼��ɽ����
��3���Ƿֶκ�������1��t$��\frac{4}{3}$ʱ����ͼ1�и���S=S��KGB��⣬��$\frac{4}{3}$��t��2ʱ����ͼ2�У���ML��AB��L���ӳ�ML��PQ��T������S=S��MGL+S����MLBK��⣬��2��t��3ʱ����ͼ3�У�����S=S����HGRK��⣮
��4���ֵ�ON=OGʱ��ON=NGʱ�ֱ��г����̼��ɽ�����⣮
��� �⣻��1�����߶�PM������Bʱ��t=$\frac{2}{2}$=1s��
��t=1sʱ���߶�PM������B
��2������P�ӵ�E�˶���Oʱ����M���������߶�AB�ϣ�
����P�ӵ�O���E�˶�ʱ����M���߶�AB��ʱ����2t+t=12��t=4s��
��t=4sʱ����M���߶�AB�ϣ�
��3����ͼ1�У���PM��AB��BC��G��K���ӳ�CB��PQ��H����PH=KH=2t-1��
����M���߶�BC��ʱ��2t-1=3-t�����t=$\frac{4}{3}$��
��1��t$��\frac{4}{3}$ʱ��S=S��KGB=$\frac{1}{2}$��2t-2��2=2��t-2��2��
��QM������Bʱ��t=2����ʱ��M���߶�CD�ϣ�
��$\frac{4}{3}$��t��2ʱ����ͼ2�У���ML��AB��L���ӳ�ML��PQ��T����S=S��MGL+S����MLBK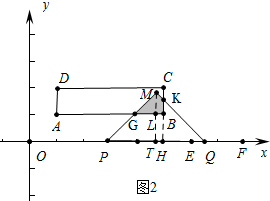
��PT=TQ=MT=$\frac{1}{2}$��2t+2-t��=$\frac{1}{2}$��t+2����
��ML=GL=$\frac{1}{2}$��t+2��-1=$\frac{1}{2}$t��HT=LB=$\frac{1}{2}$��t+2��-��3-t��=$\frac{3}{2}t$-2��KB=HK-1=2-t��
��S=$\frac{1}{2}$•��$\frac{1}{2}$t��2+$\frac{1}{2}$��$\frac{1}{2}$t+2-t��•��$\frac{3}{2}$t-2��=-$\frac{1}{4}$t2+2t-2
��2��t��3ʱ����ͼ3�У�S=S����HGRK��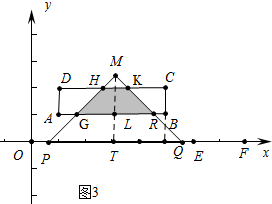
��GR=PQ-2��HK=PQ-4��
��GR=t��KH=t-2��
��S=$\frac{1}{2}$��t+t-2��•1=t-1��
��������S=$\left\{\begin{array}{l}{2��t-2��^{2}}&{��1��t��\frac{4}{3}��}\\{-\frac{1}{4}{t}^{2}+2t-2}&{��\frac{4}{3}��t��2��}\\{t-1}&{��2��t��3��}\end{array}\right.$��
��4����ͼ4�У�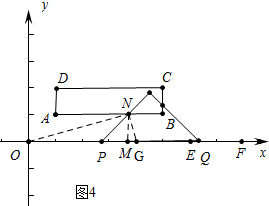
��ON=OGʱ����NM��OG����ΪM��
��OG=ON=4��OM=$\sqrt{O{N}^{2}-N{M}^{2}}$=$\sqrt{15}$��
��PM=NM=1��
��OP=$\sqrt{15}$-1��
��6-2t=$\sqrt{15}$-1��2t-6=$\sqrt{15}$-1��
��t=$\frac{7-\sqrt{15}}{2}$��$\frac{5+\sqrt{15}}{2}$������������������
��ON=NGʱ��OM=MG=2��OP=1��
��6-2t=1��2t-6=1��
��t=$\frac{5}{2}$��$\frac{7}{2}$��
��������t=$\frac{7-\sqrt{15}}{2}$��$\frac{5}{2}$��$\frac{7}{2}$ʱ����ONG�ǵ��������Σ�
���� ���⿼���ı����ۺ��⣬���������ε����ʡ����ɶ���������Ĺؼ����ҵ��ؼ��㣬ѧ����ȷ����ͼ�Σ�ѧ�����ӳ��ø����ߣ�ѧ��������۵�˼�룬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪��һ��ԽҰ���У���С������1600��ʱ��Сǿ����1400�ף�С����Сǿ�˺����ܵ�·��y���ף���ʱ��t���룩֮��ĺ�����ϵ��ͼ��ʾ��
��֪��һ��ԽҰ���У���С������1600��ʱ��Сǿ����1400�ף�С����Сǿ�˺����ܵ�·��y���ף���ʱ��t���룩֮��ĺ�����ϵ��ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
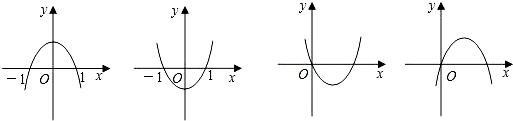 ��a��bΪ��������b��0��������y=ax2+bx+a2-5a-6Ϊ����ͼ��֮һ����a��ֵΪ��������
��a��bΪ��������b��0��������y=ax2+bx+a2-5a-6Ϊ����ͼ��֮һ����a��ֵΪ��������| A�� | 6��-1 | B�� | -6�� 1 | C�� | 6 | D�� | -1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 13 | B�� | 14 | C�� | 15 | D�� | 16 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2cm | B�� | 6cm | C�� | 8cm | D�� | 2cm��8cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 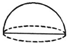 ���� | B�� | 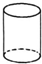 Բ�� | C�� | 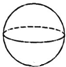 �� | D�� |  ������ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com