
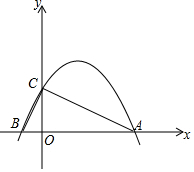
 ��ͼ��������y=ax2+bx+2��x����A��B���㣬��y���ڵ�C����BCO=��CAB��tan��BCO=$\frac{1}{2}$
��ͼ��������y=ax2+bx+2��x����A��B���㣬��y���ڵ�C����BCO=��CAB��tan��BCO=$\frac{1}{2}$���� ��1������ȷ��A��B��C�������꣬�����ô���ϵ�������ɽ�����⣮
��2���������ߵĶ���ƽ����x����ʱ�������ߵĽ���ʽy=-$\frac{1}{2}$��x-$\frac{3}{2}$��2=-$\frac{1}{2}$x2+$\frac{3}{2}$x-$\frac{9}{8}$����ʱ���������߶�OAֻ��1�����㣬��ʱt=$\frac{25}{8}$����ƽ�ƺ�������߾�����Oʱ�����������߶�OA���������㣬��ʱt=2�����ͼ�ɽ�����⣮
��3������ͼ������C��CP��AB����������P����ʱ��PCA=��CAB����������P��3��2����������߶�AC�Ĵ�ֱƽ���ߵĽ���ʽ��CP�Ľ���G��ֱ��AG�������ߵĽ���ΪP�䣬��ʱ��P��AC=��PCA=��CAB�����ֱ��AG�Ľ���ʽ���ⷽ���鼴�������P�����꣮
��� �⣺��1������������y=ax2+bx+2����x=0����y=2��
��C��0��2����
��OC=2��
�ߡ�BCO=��CAB��tan��BCO=$\frac{1}{2}$��
��$\frac{BO}{CO}$=$\frac{OC}{OA}$=$\frac{1}{2}$��
��OB=1��OA=4��
��B��-1��0����A��4��0����
��A��B�����������y=ax2+bx+2��$\left\{\begin{array}{l}{a-b+2=0}\\{16a+4b+2=0}\end{array}\right.$���$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=\frac{3}{2}}\end{array}\right.$��
�������ߵĽ���ʽΪy=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2��
��2����y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2=-$\frac{1}{2}$��x-$\frac{3}{2}$��2+$\frac{25}{8}$��
�ඥ������Ϊ��$\frac{3}{2}$��$\frac{25}{8}$����
�������ߵĶ���ƽ����x����ʱ�������ߵĽ���ʽy=-$\frac{1}{2}$��x-$\frac{3}{2}$��2=-$\frac{1}{2}$x2+$\frac{3}{2}$x-$\frac{9}{8}$����ʱ���������߶�OAֻ��1�����㣬��ʱt=$\frac{25}{8}$��
��ƽ�ƺ�������߾�����Oʱ�����������߶�OA���������㣬��ʱt=2��
��ͼ���֪����0��t��2��t=$\frac{25}{8}$ʱ�����������߶�OA����ֻ��һ�����㣮
��3����ͼ������C��CP��AB����������P����ʱ��PCA=��CAB����������P��3��2����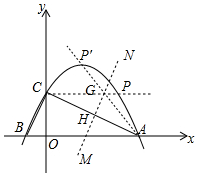
��A��4��0����C��0��2����
���߶�AC���е�H���꣨2��1����
��ֱ��AC�Ľ���ʽΪy=-$\frac{1}{2}$x+2����H��ֱAC��ֱ��MN�Ľ���ʽΪy=2x-3��
��ֱ��MN��PC�Ľ���GΪ��$\frac{5}{2}$��2������ֱ��AG�������ߵĽ���ΪP�䣬
��GC=GA��
���P��AC=��PCA=��CAB��
��A��4��0����G��$\frac{5}{2}$��2����
��ֱ��AG����ʽΪy=-$\frac{4}{3}$x+$\frac{16}{3}$��
��$\left\{\begin{array}{l}{y=-\frac{1}{2}{x}^{2}+\frac{3}{2}x+2}\\{y=-\frac{4}{3}x+\frac{16}{3}}\end{array}\right.$���$\left\{\begin{array}{l}{x=4}\\{y=0}\end{array}\right.$��$\left\{\begin{array}{l}{x=\frac{5}{3}}\\{y=\frac{28}{9}}\end{array}\right.$��
���P��������$\frac{5}{3}$��$\frac{28}{9}$����
�������������������ĵ�P����Ϊ��3��2����$\frac{5}{3}$��$\frac{28}{9}$����
���� ���⿼����κ����ۺ��⡢һ�κ���������ϵ������ƽ���ߵ����ʣ��߶εĴ�ֱƽ���ߵ����ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�����÷����������꣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{5}{2}$��y��$\frac{3}{2}$ | B�� | $\frac{3}{2}$��y��$\frac{5}{2}$ | C�� | $\frac{3}{2}$��y��$\frac{5}{2}$ | D�� | $\frac{3}{2}$��y��$\frac{5}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com