
【题目】已知抛物线y=﹣![]() x2﹣(m+3)x+m2﹣12与x轴交于A(x1,0)、B(x2,0)两点,且x1<0,x2>0,抛物线与y轴交于点C,OB=2OA.
x2﹣(m+3)x+m2﹣12与x轴交于A(x1,0)、B(x2,0)两点,且x1<0,x2>0,抛物线与y轴交于点C,OB=2OA.
(1)求抛物线解析式;
(2)已知直线y=![]() x+2与抛物线相交于M、N两点,分别过M、N作x轴的垂线,垂足为M1、N1,是否存在点P,同时满足如下两个条件:
x+2与抛物线相交于M、N两点,分别过M、N作x轴的垂线,垂足为M1、N1,是否存在点P,同时满足如下两个条件:
①P为抛物线上的点,且在直线MN上方;
②![]() :
:![]() =6:35
=6:35
若存在,则求点P横坐标t,若不存在,说明理由.

【答案】(1)y=﹣![]() x2+x+4 (2)存在,t=
x2+x+4 (2)存在,t=![]() 或t=﹣1
或t=﹣1
【解析】
(1)先求出x2=﹣2x1,再令y=0,用根与系数的关系得出x1+x2=﹣2(m+3),x1x2=﹣2(m2﹣12),即可得出结论;
(2)先求出M,N的坐标,进而求出梯形MM1N1N的面积,即可求出三角形PMN的面积,进而求出t的值,最后判断即可得出结论.
解:(1)∵A(x1,0)、B(x2,0)且x1<0,x2>0,
∴OA=﹣x1,OB=x2,
∵OB=2OA,
∴x2=﹣2x1,
∵抛物线y=﹣![]() x2﹣(m+3)x+m2﹣12与x轴交于A(x1,0)、B(x2,0)两点,
x2﹣(m+3)x+m2﹣12与x轴交于A(x1,0)、B(x2,0)两点,
令y=0,
∴0=﹣![]() x2﹣(m+3)x+m2﹣12,
x2﹣(m+3)x+m2﹣12,
∴x2+2(m+3)x﹣2(m2﹣12)=0,
根据根与系数关系得,x1+x2=﹣2(m+3),x1x2=﹣2(m2﹣12),
∴﹣x1=﹣2(m+3),﹣2x12=﹣2(m2﹣12),
∴4(m+3)2=m2﹣12,∴m=﹣4,
∴抛物线解析式为y=﹣![]() x2+x+4;
x2+x+4;
(2)如图,由(1)知,抛物线解析式为y=﹣![]() x2+x+4①,
x2+x+4①,

∴直线y=![]() x+2②与抛物线相交于M、N两点,
x+2②与抛物线相交于M、N两点,
联立①②解得,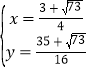 或
或 ,
,
∴N(![]() ,
,![]() ),M(
),M(![]() ,
,![]() ),
),
∴MM1=![]() ,NN1=
,NN1=![]() ,M1N1=
,M1N1=![]() ,
,
∴S梯形MM1N1N=![]() (MM1+NN1)×M1N1=
(MM1+NN1)×M1N1=![]() ,
,
∵![]() :
:![]() =6:35,
=6:35,
∴S△PMN=![]() ,
,
设P(t,﹣![]() t2+t+4),(
t2+t+4),(![]() <t<
<t<![]() ),
),
∴Q(t,![]() t+2),
t+2),
∴PQ=﹣![]() t2+t+4﹣
t2+t+4﹣![]() t﹣2=﹣
t﹣2=﹣![]() t2+
t2+![]() t+2,
t+2,
∴S△PMN=![]() PQM1N1=
PQM1N1=![]() (﹣
(﹣![]() t2+
t2+![]() t+2)×
t+2)×![]() =
=![]() ,
,
∴2t2﹣3t﹣5=0,
∴t=![]() 或t=﹣1,都符合题,
或t=﹣1,都符合题,
即:点P横坐标t=![]() 或t=﹣1.
或t=﹣1.
注:【利用估算的方法将t的范围缩放】
∵8.5<![]() <8.6,
<8.6,
∴﹣1.4<![]() <﹣1.3,
<﹣1.3,
2.875<![]() <2.9,
<2.9,
∵![]() <t<
<t<![]() ,
,
∴﹣1.3<t<2.875.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=ax2+bx+3交x轴于A(﹣1,0)和B(5,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,过点C作CF⊥l于F.
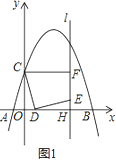
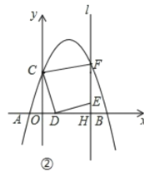
(1)求抛物线解析式;
(2)如图②,当点F恰好在抛物线上时,求线段OD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
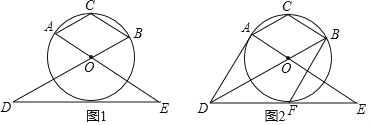
【题目】如图1,AOBC的顶点A、B、C在⊙O上,点D、E分别在BO、AO的延长线上,且OD=2OB,OE=2OA,连接DE.
(1)求∠AOB的度数;
(2)求证:DE是⊙O的切线;
(3)如图2,设直线DE与⊙O相切于点F,连接AD、BF,判断线段AD与BF的位置关系和数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC平分∠DAB,AC2=ABAD,∠ADC=90°,点E为AB的中点.
(1)求证:△ADC∽△ACB.
(2)若AD=2,AB=3,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B两点的坐标分别为A(0,2![]() ),B(2,0),直线AB与反比例函数y=
),B(2,0),直线AB与反比例函数y=![]() 的图象相交于点C和点D,将△OBC绕点O逆时针方向旋转θ角(θ为锐角),得到△OB′C′,当θ=_____时,OC′⊥AB;
的图象相交于点C和点D,将△OBC绕点O逆时针方向旋转θ角(θ为锐角),得到△OB′C′,当θ=_____时,OC′⊥AB;

查看答案和解析>>
科目:初中数学 来源: 题型:
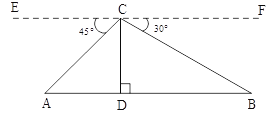
【题目】如图,从热气球C处测得地面A、B两点的俯角分别为45°、30°,如果此时热气球C处离地面的高度CD为100米,且点A、D、B在同一直线上,求AB两点间的距离(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为反比例函数y=![]() 的图像上一点,PA⊥x轴于点A,△PAO的面积为6,则下列各点中也在这个反比例函数图像上的是( )
的图像上一点,PA⊥x轴于点A,△PAO的面积为6,则下列各点中也在这个反比例函数图像上的是( )

A. (2,3) B. (﹣2,6) C. (2,6) D. (﹣2,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,交OA于点F,连接EF并延长EF交AB于G,且EG⊥AB.
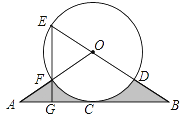
(1)求证:直线AB是⊙O的切线;
(2)若EF=2FG,AB= ![]() ,求图中阴影部分的面积;
,求图中阴影部分的面积;
(3)若EG=9,BG=12,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮利用三张卡片做游戏,卡片上分别写有A,B,B.这些卡片除字母外完全相同,从中随机摸出一张,记下字母后放回,充分洗匀后,再从中摸出一张,如果两次摸到卡片字母相同则小明胜,否则小亮胜,这个游戏对双方公平吗?请说明现由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com