
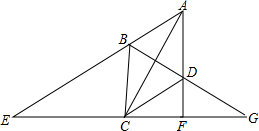
 如图.菱形ABCD,AE=3AF,求证:BG=3DG.
如图.菱形ABCD,AE=3AF,求证:BG=3DG. 分析 由CD∥AE知△CDF∽△EAF,从而得出$\frac{AF}{AE}=\frac{DF}{DC}=\frac{1}{3}$,根据BC=CD得$\frac{DF}{BC}=\frac{1}{3}$,再由BC∥DF知△DFG∽△BCG,即可得$\frac{DF}{BC}=\frac{DG}{BG}=\frac{1}{3}$,从而得证.
解答 证明:∵四边形ABCD是菱形,
∴CD∥AE,
∴△CDF∽△EAF,
∵AE=3AF,
∴$\frac{AF}{AE}=\frac{DF}{DC}=\frac{1}{3}$,
∵BC=CD,
∴$\frac{DF}{BC}=\frac{1}{3}$,
又∵BC∥DF,
∴△DFG∽△BCG,
∴$\frac{DF}{BC}=\frac{DG}{BG}=\frac{1}{3}$,
∴BG=3DG.
点评 本题主要考查相似三角形的判定与性质及菱形的性质,熟练掌握预备定理是解题的关键.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:解答题
 为了解某县2014年初中毕业生的实验成绩等级的分布情况,随机抽取了该县若干名学生的实验成绩进行统计分析,并根据抽取的成绩绘制了如图所示的统计图表:
为了解某县2014年初中毕业生的实验成绩等级的分布情况,随机抽取了该县若干名学生的实验成绩进行统计分析,并根据抽取的成绩绘制了如图所示的统计图表:| 成绩等级 | A | B | C | D |
| 人数 | 60 | x | y | 10 |
| 百分比 | 30% | 50% | 15% | m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直角△ABC中,AB=5,BC=3,AC=4,直角△ABC将沿着它的一条边AB旋转一周,得到一个什么图形?试求出其表面积和点C运动的路程.
如图,直角△ABC中,AB=5,BC=3,AC=4,直角△ABC将沿着它的一条边AB旋转一周,得到一个什么图形?试求出其表面积和点C运动的路程.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知在纸面上有一数轴(如图),折叠纸面.例如:若数轴上数2表示的点与数-2表示的点重合,则数轴上数-4表示的点与数4表示的点重合,根据你对例题的理解,解答下列问题:
已知在纸面上有一数轴(如图),折叠纸面.例如:若数轴上数2表示的点与数-2表示的点重合,则数轴上数-4表示的点与数4表示的点重合,根据你对例题的理解,解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com