
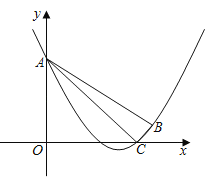
【题目】如图,在平面直角坐标系xOy中,抛物线y=![]() x2+mx+n经过点B(6,1),C(5,0),且与y轴交于点A.
x2+mx+n经过点B(6,1),C(5,0),且与y轴交于点A.
(1)求抛物线的表达式及点A的坐标;
(2)点P是y轴右侧抛物线上的一点,过点P作PQ⊥OA,交线段OA的延长线于点Q,如果∠PAB=45°.求证:△PQA∽△ACB;
(3)若点F是线段AB(不包含端点)上的一点,且点F关于AC的对称点F′恰好在上述抛物线上,求FF′的长.
【答案】(1)y=![]() x2﹣
x2﹣![]() x+5,点A坐标为(0,5);(2)详见解析;(3)
x+5,点A坐标为(0,5);(2)详见解析;(3)![]() .
.
【解析】
(1)将点B、C代入抛物线解析式y=![]() x2+mx+n即可;
x2+mx+n即可;
(2)先证△ABC为直角三角形,再证∠QAP+∠CAB=90°,又因∠AQP=∠ACB=90°,即可证△PQA∽△ACB;
(3)做点B关于AC的对称点B',求出BB'的坐标,直线AB'的解析式,即可求出点F'的坐标,接着求直线FF'的解析式,求出其与AB的交点即可.
解:(1)将B(6,1),C(5,0)代入抛物线解析式y=![]() x2+mx+n,
x2+mx+n,
得
解得,m=﹣![]() ,n=5,
,n=5,
则抛物线的解析式为:y=![]() x2﹣
x2﹣![]() x+5,点A坐标为(0,5);
x+5,点A坐标为(0,5);
(2)∵AC=![]() ,BC=
,BC=![]() ,AB=
,AB=![]() ,
,
∴AC2+BC2=AB2,
∴△ABC为直角三角形,且∠ACB=90°,
当∠PAB=45°时,点P只能在点B右侧,过点P作PQ⊥y 轴于点Q,
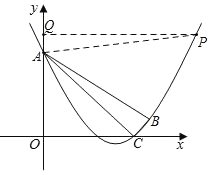
∴∠QAB+∠OAB=180°﹣∠PAB=135°,
∴∠QAP+∠CAB=135°﹣∠OAC=90°,
∵∠QAP+∠QPA=90°,∴∠QPA=∠CAB,
又∵∠AQP=∠ACB=90°,∴△PQA∽△ACB;
(3)做点B关于AC的对称点B',则A,F',B'三点共线,
由于AC⊥BC,根据对称性知点B'(4,﹣1),
将B'(4,﹣1)代入直线y=kx+5,
∴k=﹣![]() ,∴yAB'=﹣
,∴yAB'=﹣![]() x+5,
x+5,
联立 解得,x1=
解得,x1=![]() ,x2=0(舍去),
,x2=0(舍去),
则F'(![]() ,﹣
,﹣![]() ),
),
将B(6,1),B'(4,﹣1)代入直线y=mx+n,
得,![]() 解得,
解得,![]() ∴yBB'=x﹣5,
∴yBB'=x﹣5,
由题意知,kFF'=KBB',∴设yFF'=x+b,
将点F'(![]() ,﹣
,﹣![]() )代入,得,b=﹣
)代入,得,b=﹣![]() ,
,
∴yFF'=x﹣![]() ,
,
联立 解得,
解得,
∴F(![]() ,
,![]() ),
),
则FF'=![]() =
=![]() .
.



 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案科目:初中数学 来源: 题型:
【题目】某文具店购进一批纪念册,每本进价为20元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间具有某种函数关系,其对应规律如下表所示
售价x(元/本) | … | 22 | 23 | 24 | 25 | 26 | 27 | … |
销售量y(件) | … | 36 | 34 | 32 | 30 | 28 | 26 | … |
(1)请直接写出y与x的函数关系式: .
(2)设该文店每周销售这种纪念册所获得的利润为W元,写出W与x之间的函数关系式,并求出该纪念册的销售单价定为多少元时,才能使文具店销售该纪念册每周所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
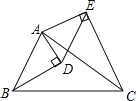
【题目】在△ABC中,分别以AB,AC为斜边作Rt△ABD和Rt△ACE,∠ADB=∠AEC=90°,∠ABD=∠ACE=30°,连接DE.若DE=5,则BC长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中装有4张卡片,分别印有数字1、2、3、6,这4张卡片除印有的数字不同外,其余都相同.
(1)搅匀后从中任意摸出1张卡片,摸到印有奇数卡片的概率为_______;
(2)搅匀后从中任意摸出1张卡片,将该卡片印有的数字记为![]() ,再从剩余3张卡片中任意摸出1张卡片,将该卡片印有的数字记为
,再从剩余3张卡片中任意摸出1张卡片,将该卡片印有的数字记为![]() ,请用列表或画树状图的方法求出点
,请用列表或画树状图的方法求出点![]() 在反比例函数
在反比例函数![]() 图像上的概率.
图像上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
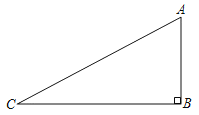
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=4,点P在边BC上,联结AP,将△ABP绕着点A旋转,使得点P与边AC的中点M重合,点B的对应点是点B′,则BB′的长等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题 :如图1,在四边形![]() 中,点
中,点![]() 为
为![]() 上一点,∠
上一点,∠![]() =∠
=∠![]() =∠
=∠![]() =90°,求证:
=90°,求证:![]() .
.

(2)探究:如图2,在四边形![]() 中,点
中,点![]() 为
为![]() 上一点,当∠
上一点,当∠![]() =∠
=∠![]() =∠
=∠![]() 时,上述结论是否依然成立?说明理由.
时,上述结论是否依然成立?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
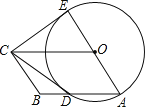
【题目】如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,
(1)求证:CD是⊙O的切线;
(2)若BC=3,AB=5,求平行四边形OABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
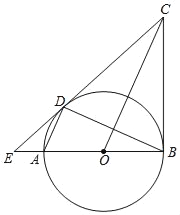
【题目】如图,已知AB为⊙O的直径,AD,BD是⊙O的弦,BC是⊙O的切线,切点为B,OC∥AD,BA,CD的延长线相交于点E.
(1)求证:DC是⊙O的切线;
(2)若⊙O半径为4,∠OCE=30°,求△OCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=(m-2)x2+(m+3)x+m+2的图象过点(0,5)
(1)求m的值,并写出二次函数的表达式;
(2)求出二次函数图象的顶点坐标、对称轴。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com