
【题目】解方程组:(1)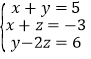 ;
;
(2)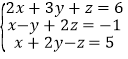 ;
;
(3)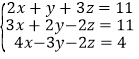 ;
;
(4)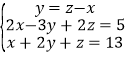 .
.
【答案】(1) ;(2)
;(2)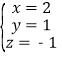 ;(3)
;(3)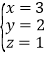 ;(4)
;(4)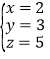 .
.
【解析】
(1)由①-②消去x,与③组成y、z的二元一次方程组,进一步解二元一次方程组,求得答案即可;
(2)③+①消去z,③×2+②消去z,组成关于x、y的二元一次方程组,进一步解二元一次方程组,求得答案即可;
(3)①×2-②消去y,①×3+③消去y,组成关于x、z的二元一次方程组,进一步解二元一次方程组,求得答案即可;
(4)把①代入②消去y,把①代入③,消去y,组成关于x、z的二元一次方程组,进一步解二元一次方程组,求得答案即可.
(1)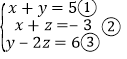
由①-②,得y-z=8.④
④-③,得z=2.
把z=2代入④,得y=10.把y=10代入①,得x=-5.
所以,原方程组的解为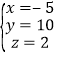 ;
;
(2)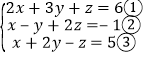
③+①,得3x+5y=11.④
③×2+②,得3x+3y=9.⑤
④-⑤,得2y=2,y=1.
将y=1代入⑤,得3x=6,x=2.
将x=2,y=1代入①,得z=6-2×2-3×1=-1,
所以原方程组的解为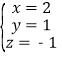 ;
;
(3)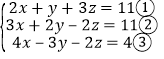 ,
,
①×2-②,得x+8z=11.④
①×3+③,得10x+7z=37.⑤
解由④与⑤组成的方程组,得![]() ,
,
把x=3,z=1代入①,得y=2.
所以原方程组的解为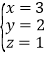 ;
;
(4)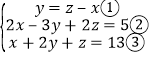 ,
,
把①代入②,得2x-3z+3x+2z=5,
即5x-z=5④
把①代入③,得x+2z-2x+z=13,
即3z-x=13.⑤
④×3+⑤,得14x=28,所以x=2.
把x=2代入④,得z=5.
把x=2,z=5代入①,得y=3.
所以原方程组的解是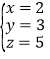


科目:初中数学 来源: 题型:
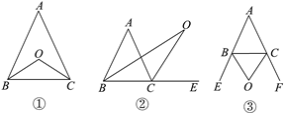
【题目】探索三角形的内角与外角平分线(三角形的外角是三角形的一边与另一边的延长线所组成的角):
(1)如图①,在△ABC中,BO平分∠ABC,CO平分∠ACB,若∠A=50°,则∠BOC=________;此时∠A与∠BOC有怎样的关系?试说明理由.
(2)如图②,BO平分∠ABC,CO平分∠ACE,若∠A=50°,则∠BOC=________;此时∠A与∠BOC有怎样的关系?试说明理由.
(3)如图③,△ABC的外角∠CBE,∠BCF的平分线BO,CO相交于点O,若∠A=50°,则∠BOC=______;此时∠A与∠BOC有怎样的关系?(不需说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(﹣8,0),点P的坐标为 ![]() ,直线y=
,直线y= ![]() x+b过点A,交y轴于点B,以点P为圆心,以PA为半径的圆交x轴于点C.
x+b过点A,交y轴于点B,以点P为圆心,以PA为半径的圆交x轴于点C.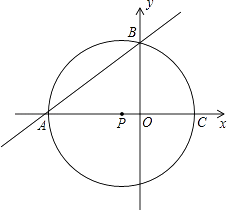
(1)判断点B是否在⊙P上?说明理由.
(2)求过A、B、C三点的抛物线的解析式;并求抛物线与⊙P另外一个交点为D的坐标.
(3)⊙P上是否存在一点Q,使以A、P、B、Q为顶点的四边形是菱形?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,正方形OABC的面积为16,点D的坐标为(0,3).将直线BD沿y轴向下平移d个单位得到直线l(0<d≤4).
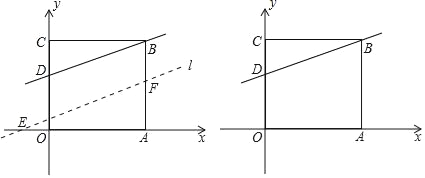
(1)则点B的坐标为 ;
(2)当d=1时,求直线l的函数表达式;
(3)设直线l与x轴相交于点E,与边AB相交于点F,若CE=CF,求d的值并直接写出此时∠ECF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
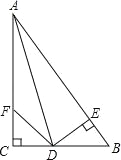
【题目】如图,在△ABC中,∠C=90°,∠CAD=∠BAD,DE⊥AB于E,点F在边AC上,连接DF.
(1)求证:AC=AE;
(2)若AC=8,AB=10,且△ABC的面积等于24,求DE的长;
(3)若CF=BE,直接写出线段AB,AF,EB的数量关系:_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC⊥CD,∠BED=90°.填空:
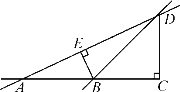
(1)∠ACD=_____度;
(2)直线AD与BE的位置关系是__________;
(3)点B到直线AD的距离是线段________的长度,点D到直线AB的距离是线段______的长度;
(4)在线段DA,DB,DC中,最短的是线段______;在线段BA,BE,BD中,最短的是线段______,理由是_____________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在⊙O上,∠CAB的平分线交⊙O于点D,过点D作AC的垂线交AC的延长线于点E,连接BC交AD于点F. 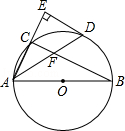
(1)猜想ED与⊙O的位置关系,并证明你的猜想;
(2)若AB=6,AD=5,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
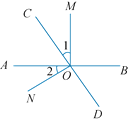
【题目】如图,直线AB,CD相交于点O,过点O作两条射线OM,ON,且∠AOM=∠CON=90°.
(1)若OC平分∠AOM,求∠AOD的度数;
(2)若∠1=∠BOC,求∠AOC和∠MOD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com