
【题目】(1)引入:
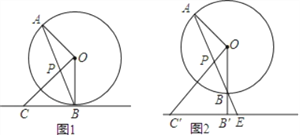
如图1,直线AB为⊙O的弦,OC⊥OA,交AB于点P,且PC=BC,直线BC是否与⊙O相切,为什么?
(2)引申:
如图2,记(1)中⊙O的切线为直线l,在(1)的条件下,将切线l向下平移,设平移后的直线l与OB的延长线相交于点B′,与AB的延长线相交于点E,与OP的延长线相交于点C′,找出图2中与C′P相等的线段,并说明理由.
【答案】(1)相切,(2)C′P=C′E.
【解析】试题分析:(1)由OC⊥OA,易得∠APO+∠OAB=90°,然后由等腰三角形的性质可得∠OAB=∠ABO,∠CBP=∠CPB,等量代换可得∠CBP+∠OBA=90°,即∠OBC-90°,由切线的判定可得出结论;
(2)由(1)可得∠OAB+∠C′PE=90°,等量代换可得∠ABO+∠C′PE=90°,由∠EBB′+∠BEB′=90°,∠EBB′=∠ABO,易得∠C′PE=∠BEB′,得出结论.
试题解析:(1)相切,
∵OC⊥OA,
∴∠AOC=90°,
∴∠APO+∠OAB=90°,
∵OA=OB,
∴∠OAB=∠ABO,
∵PC=PB,
∴∠CBP=∠CPB,
∵∠APO=∠CPB,
∴∠CBP+∠OBA=90°,
即∠OBC=90°,
∴OB⊥BC
∵OB为半径,
∴BC与⊙O相切;
(2)C′P=C′E,
∵∠OB′C′=90°,∠APO+∠OAB=90°,且∠APO=∠C′PE,
∴∠OAB+∠C′PE=90°,
∵OA=OB,
∴∠OAB=∠ABO,
∴∠ABO+∠C′PE=90°,
∵∠EBB′+∠BEB′=90°,且∠EBB′=∠ABO,
∴∠C′PE=∠BEB′,
∴C′P=C′E.


科目:初中数学 来源: 题型:
【题目】如图,一张纸片的形状为直角三角形,其中∠C=90°,AC=12cm,BC=16cm,沿直线AD折叠该纸片,使直角边AC与斜边上的AE重合,则CD的长为cm. 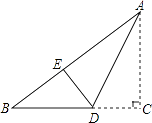
查看答案和解析>>
科目:初中数学 来源: 题型:
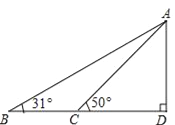
【题目】据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪,如图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°.
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.(tan31°≈0.6,tan50°≈1.2,结果精确到1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明有5张写着不同的数字的卡片,请你按要求抽出卡片,完成下列各问题:
![]()
(1)从中取出2张卡片,使这2张卡片上数字乘积最大,最大值是 ;
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,最小值是 ;
(3)从中取出4张卡片,用学过的运算方法,使结果为24.写出运算式子:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】满足下列条件的四边形不是正方形的是( )
A. 对角线相互垂直的矩形 B. 对角线相等的菱形
C. 对角线相互垂直且相等的四边形 D. 对角线垂直且相等的平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次夏令营活动中,小霞同学从营地A点出发,要到距离A点10千米的C地去,先沿北偏东70°方向走了8千米到达B地,然后再从B地走了6千米到达目的地C,此时小霞在B地的( ) 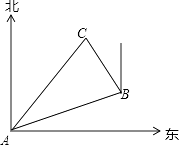
A.北偏东20°方向上
B.北偏西20°方向上
C.北偏西30°方向上
D.北偏西40°方向上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某鞋店销售一款新式女鞋,试销期间对该款不同型号的女鞋销售量统计如下表:
尺码/厘米 | 22 | 22.5 | 23 | 23.5 | 24 | 24.5 | 25 |
销售量/双 | 1 | 2 | 3 | 11 | 8 | 6 | 4 |
该店经理如果想要了解哪种女鞋的销售量最大,那么他应关注的统计量是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com