
科目:初中数学 来源: 题型:解答题
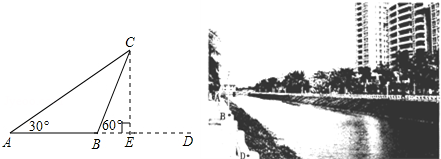
 如图,已知AD是△ABC的高,点E、G分别在AB、AC上,EF⊥BC,垂足为F,∠CGD=∠BAC,若∠1=50°,求∠2和∠B的度数.
如图,已知AD是△ABC的高,点E、G分别在AB、AC上,EF⊥BC,垂足为F,∠CGD=∠BAC,若∠1=50°,求∠2和∠B的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 购物总金额(原价) | 优惠率 |
| 不超过5000元的部分 | 10% |
| 超过5000元且不超过10000元的部分 | 20% |
| 超过10000元且不超过20000元的部分 | 30% |
| … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
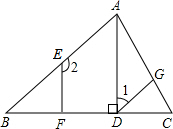
 如图,为修铁路需凿隧道AC,测得∠A+∠B=90°,AB=130m,BC=120m,若每天凿隧道5m,则把隧道凿通需要( )
如图,为修铁路需凿隧道AC,测得∠A+∠B=90°,AB=130m,BC=120m,若每天凿隧道5m,则把隧道凿通需要( )| A. | 10天 | B. | 9天 | C. | 8天 | D. | 11天 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
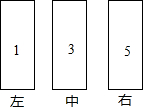 如图所示,三根音管被敲击时能依次发出“1”“3”“5”,两只音锤同时从“1”开始,以相同的节拍往复敲击这三根音管,不同的是:甲锤每拍移动一位(左中右中左中右…),乙锤则在两端各有一拍不移位(左中右右中左左中右…).第2012拍时,听到相同的音,这个相同的音是3.
如图所示,三根音管被敲击时能依次发出“1”“3”“5”,两只音锤同时从“1”开始,以相同的节拍往复敲击这三根音管,不同的是:甲锤每拍移动一位(左中右中左中右…),乙锤则在两端各有一拍不移位(左中右右中左左中右…).第2012拍时,听到相同的音,这个相同的音是3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
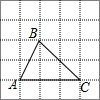 如图,每个小方格都是边长为1的小正方形,△ABC是格点三角形(即顶点恰好是小正方形的顶点),在图中与△ABC不重叠且有一条公共边的全等的所有格点三角形的个数是( )
如图,每个小方格都是边长为1的小正方形,△ABC是格点三角形(即顶点恰好是小正方形的顶点),在图中与△ABC不重叠且有一条公共边的全等的所有格点三角形的个数是( )| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com