
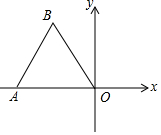
 如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为2的等边三角形.
如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为2的等边三角形.分析 (1)作高线BC,根据等边三角形的性质和勾股定理求OC和BC的长,写出三点的坐标,注意象限的符号问题;
(2)如图2,由旋转可知:A′与B重合,B与B′关于y轴对称,可得:A′,B′的坐标.
解答 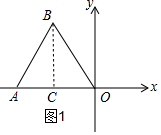 解:(1)如图1,过B作BC⊥OA于C,
解:(1)如图1,过B作BC⊥OA于C,
∵△AOB是等边三角形,且OA=2,
∴OC=$\frac{1}{2}$OA=1,
由勾股定理得:BC=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴A(-2,0),B(-1,$\sqrt{3}$),O(0,0);
(2)如图2,∵∠AOB=60°,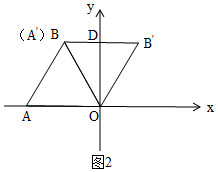 OA=OB,
OA=OB,
∴A′与B重合,
∴A′(-1,$\sqrt{3}$),
由旋转得:∠BOB′=60°,OB=OB′,
∵∠AOD=90°,
∴∠BOD=30°,
∴∠DOB′=30°,
∴BB′⊥OD,DB=DB′,
∴B′(1,$\sqrt{3}$).
点评 本题考查了坐标与图形变换、等边三角形的性质、旋转的性质,熟练掌握旋转和等边三角形的性质是关键,并注意点所在象限的符号问题.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:解答题
 如图,直线DE与直线AB、CD分别交于点E、D、EG平分∠DEB,直线GF与直线AB交于点F,若∠CDE=116°,∠AFG=130°,∠G=8°.判断直线AB、CD是否平行?并说明理由.
如图,直线DE与直线AB、CD分别交于点E、D、EG平分∠DEB,直线GF与直线AB交于点F,若∠CDE=116°,∠AFG=130°,∠G=8°.判断直线AB、CD是否平行?并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
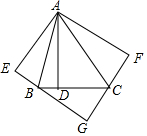 如图,在△ABC中,∠BAC=45°,AD⊥BC于点D,$\frac{BD}{DC}$=$\frac{2}{3}$,AD=6,将△ADB,△ADC分别沿AB,AC翻折得△ABE,△ACF,延长EB,FC相交于点G.
如图,在△ABC中,∠BAC=45°,AD⊥BC于点D,$\frac{BD}{DC}$=$\frac{2}{3}$,AD=6,将△ADB,△ADC分别沿AB,AC翻折得△ABE,△ACF,延长EB,FC相交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
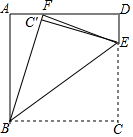 如图,正方形ABCD中,E为边CD上的一点,且CE=3DE,连接BE,将△CBE沿BE翻折,使点C落在C′处,延长BC′交AD于点F,连接EF,若AF=7,则线段EF的长为5$\sqrt{13}$.
如图,正方形ABCD中,E为边CD上的一点,且CE=3DE,连接BE,将△CBE沿BE翻折,使点C落在C′处,延长BC′交AD于点F,连接EF,若AF=7,则线段EF的长为5$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a-1>b-1 | B. | -a>-b | C. | |a|>|b| | D. | -$\frac{a}{2}$>-$\frac{b}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
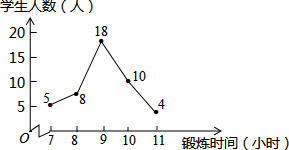 体育委员把全班45名同学的体育锻炼时间,并绘制了如图所示的折线统计图,则全班45名同学一周的体育锻炼总时间的众数和中位数分别是( )
体育委员把全班45名同学的体育锻炼时间,并绘制了如图所示的折线统计图,则全班45名同学一周的体育锻炼总时间的众数和中位数分别是( )| A. | 9,9 | B. | 9,10 | C. | 18,9 | D. | 18,18 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com