【小题1】解:(1)解:由
kx=
x+2,得(
k-1)
x=2.
依题意
k-1≠0.∴

. ……………………………………1分
∵方程的根为正整数,
k为整数,∴
k-1=1或
k-1=2.
∴
k1= 2,
k2=3. …………………………………………………2分
【小题2】(2)解:依题意,二次函数
y=
ax2-
bx+
kc的图象经过点(1,0),
∴ 0 =
a-
b+
kc,
kc =
b-
a.
∴

=

…3分
【小题3】(3)证明:方程②的判别式为Δ=(-
b)
2-4
ac=
b2-4
ac. 由
a≠0,
c≠0,得
ac≠0.
证法一:
(
i)若
ac<0,则-4
ac>0.故Δ=
b2-4
ac>0.此时方程②有两个不相等的实数根.……4分
(
ii)若
ac>0,由(2)知
a-
b+
kc =0,故
b=
a+
kc.
Δ=
b2-4
ac= (
a+
kc)
2-4
ac=
a2+2
kac+(
kc)
2-4
ac =
a2-2
kac+(
kc)
2+4
kac-4
ac=(
a-
kc)
2+4
ac(
k-1). …………………………………………………5分
∵方程
kx=
x+2的根为正实数,∴方程(
k-1)
x=2的根为正实数.
由
x>0, 2>0,得
k-1>0. …………………………………6分
∴ 4
ac(
k-1)>0. ∵(
a-
kc)
2³0,
∴Δ=(
a-
kc)
2+4
ac(
k-1)>0.此时方程②有两个不相等的实数根. …………7分
证法二:
(
i)若
ac<0,则-4
ac>0.故Δ=
b2-4
ac>0.此时方程②有两个不相等的实数根.……4分
(
ii)若
ac>0,∵抛物线
y=
ax2-
bx+
kc与
x轴有交点,
∴Δ
1=(-
b)
2-4
akc =
b2-4
akc³0.
(
b2-4
ac)-(
b2-4
akc)=4
ac(
k-1). 由证法一知
k-1>0,
∴
b2-4
ac>
b2-4
akc³0.
∴Δ=
b2-4
ac>0.此时方程②有两个不相等的实数根. …………………7分
综上,方程②有两个不相等的实数根.
证法三:由已知,

,∴
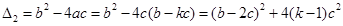
可以证明

和

不能同时为0(否则

),而

,因此

.解析:
略

 的值;
的值; . ……………………………………1分
. ……………………………………1分 =
= …3分
…3分 ,∴
,∴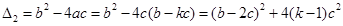
 和
和 不能同时为0(否则
不能同时为0(否则 ),而
),而 ,因此
,因此 .解析:
.解析:

 阅读快车系列答案
阅读快车系列答案
