
分析 分三种情形讨论:①当A为顶点,②当B为顶点,③当P为顶点,共有4个点P.
解答 解:如图所示,∵AO=3,BO=4,
∴在RT△AOB中,AB=$\sqrt{A{O}^{2}+B{O}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5
①当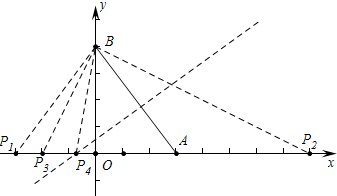 B为顶点时,BA=BP1时,P1(-3,0)
B为顶点时,BA=BP1时,P1(-3,0)
②当点A为顶点时,∵AB=AP=5,
∴P2(8,0),P3(-2,0),
③当P为顶点时,作线段AB的垂直平分线交x轴于P4,
设P4B=P4A=m,
在RT△BOP4中,m2=42+(m-3)2,解得m=$\frac{25}{6}$,
∵OP4=AP4-AO=$\frac{25}{6}-3$=$\frac{7}{6}$,
∴点P4坐标(-$\frac{7}{6}$,0).
综上所述点P的坐标为(-3,0)或(8,0)或(-2,0)或(-$\frac{7}{6}$,0).
点评 本题考查等腰三角形的定义、勾股定理等知识,学会分类讨论是解决问题的关键.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
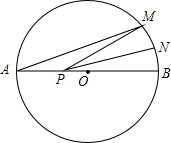 如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点,若MN=1,则△PMN周长的最小值为5.
如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点,若MN=1,则△PMN周长的最小值为5.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P在直线OB上运动且满足∠APQ=90°,PQ交x轴于点C.点D是直线OB与直线CA的交点,点E是直线CP与y轴的交点,若∠ACE=∠AEC,PD=2OD,则PA:PC=( )
如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P在直线OB上运动且满足∠APQ=90°,PQ交x轴于点C.点D是直线OB与直线CA的交点,点E是直线CP与y轴的交点,若∠ACE=∠AEC,PD=2OD,则PA:PC=( )| A. | $\frac{{\sqrt{15}}}{5}$ | B. | $\frac{{\sqrt{15}}}{3}$ | C. | $\frac{{\sqrt{15}}}{5}$或$\frac{{\sqrt{15}}}{3}$ | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
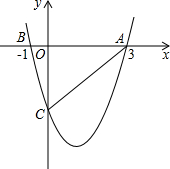 如图,二次函数y=$\frac{4}{3}$x2+bx+c的图象与x轴交于A(3,0),B(-1,0),与y轴交于点C.
如图,二次函数y=$\frac{4}{3}$x2+bx+c的图象与x轴交于A(3,0),B(-1,0),与y轴交于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com