Question

如图1，AD∥BC，AB ⊥BC于B，∠DCB=75°，以CD为边的等边△DCE的另一顶点E在线段AB上．

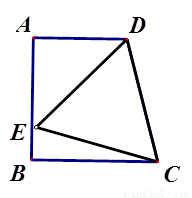
(1)填空：∠ADE=____°；

(2)求证：  AB=BC;

(3)如图2所示，若F为线段CD上一点，∠FBC=30°，求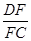的值．

 

Answer 1

【答案】

 

（1）45

（2）证明略

（3）1

【解析】解：（1）45；                                    ……2分

（2）证明：连接AC

∵∠DCB=75º，AD∥BC  

∴∠ADC=105º

      由等边△DCE可知：∠CDE =60º

故∠ADE =45º

由AB⊥BC，AD∥BC可得：∠DAB=90º

∴∠AED=45º

      ∴AD=AE                                                        

∴点A在线段DE的垂直平分线上                               ……4分

又CD=CE

∴点C也在线段DE的垂直平分线上                            ……5分

∴AC就是线段DE的垂直平分线

即AC⊥DE

∴AC平分∠EAD

∴∠BAC=45°

∴△ABC是等腰直角三角形

∴BA=BC                                                       ……6分

（3）解：连接AF，延长BF交AD的延长线于点G

∵∠FBC=30º，∠ABC=90 º

∴∠ABF=60º，∠DCB=75º

∴∠BFC=75º

故BC=BF

由(2)知：BA=BC

∴BA=BF

∴△ABF是等边三角形

∴AB=BF=FA                                                    ……7分

∴∠BAC=60 º

∴∠DAF=30 º

又∵AD∥BC

∴∠FAG=∠G=30º

∴FG =FA= FB                                                  ……8分

又∠DFG=∠CFB

∴△BCF≌△GDF（ASA）                                        ……9分

∴DF=CF

∴=1                                                       ……10分