
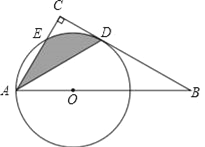
【题目】如图,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与边BC交于点D,与边AC交于点E,连接AD,且AD平分∠BAC.
(1)试判断BC与⊙O的位置关系,并说明理由;
(2)若∠BAC=60°,OA=2,求阴影部分的面积(结果保留π).
科目:初中数学 来源: 题型:
【题目】在一次数学课上,张老师出示了一个题目:“如图,ABCD的对角线相交于点O,过点O作EF垂直于BD交AB,CD分别于点F,E,连接DF,![]() 请根据上述条件,写出一个正确结论
请根据上述条件,写出一个正确结论![]() ”其中四位同学写出的结论如下:
”其中四位同学写出的结论如下:
小青:![]() ;小何:四边形DFBE是正方形;
;小何:四边形DFBE是正方形;
小夏:![]() ;小雨:
;小雨:![]() .
.
这四位同学写出的结论中不正确的是![]()
![]()

A. 小青 B. 小何 C. 小夏 D. 小雨
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业生产的一种果汁饮料由A、B两种水果配制而成,其比例与成本如下方表格所示,已知该饮料的成本价为8元/千克,按现价售出后可获利润50%,每个月可出售27500瓶.
每千克饮料所占比例 | 成本(元/千克) | |
A | 20% | m |
B | 80% | m-15 |
(1)求m的值;
(2)由于物价上涨,A水果成本提高了25%,B水果成本提高了20%,在不改变售价的情况下,若要保持每个月的利润不减少,则现在至少需要售出多少瓶饮料?
查看答案和解析>>
科目:初中数学 来源: 题型:
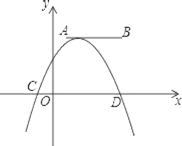
【题目】如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x+m)2+n的顶点在线段AB上,与x轴交于C,D两点(C在D的左侧),点C的横坐标最小值为﹣3,则点D的横坐标的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=50°,则∠BDE= °.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“用三角板画圆的切线”的画图过程.
如图1,已知圆上一点A,画过A点的圆的切线.
![]()

画法:(1)如图2,将三角板的直角顶点放在圆上任一点C(与点A不重合)处,使其一直角边经过点A,另一条直角边与圆交于B点,连接AB;
(2)如图3,将三角板的直角顶点与点A重合,使一条直角边经过点B,画出另一条直角边所在的直线AD.
所以直线AD就是过点A的圆的切线.
请回答:该画图的依据是_______________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ΔABC中,AB=AC,∠A=40O,延长AC到D,使CD=BC,点P是ΔABD的内心,则∠BPC=

A. 105° B. 110° C. 130° D. 145°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,且对称轴为直线
点,且对称轴为直线![]() ,点
,点![]() 坐标为
坐标为![]() .则下面的四个结论:①
.则下面的四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④当
;④当![]() 时,
时,![]() 或
或![]() .其中正确的是( )
.其中正确的是( )

A.①②B.①③C.①④D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践操作
如图,![]() 是直角三角形,
是直角三角形,![]() ,利用直尺和圆规按下列要求作图,并在图中表明相应的字母.(保留作图痕迹,不写作法)
,利用直尺和圆规按下列要求作图,并在图中表明相应的字母.(保留作图痕迹,不写作法)
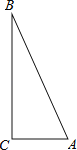
(1)①作![]() 的平分线,交
的平分线,交![]() 于点
于点![]() ;②以
;②以![]() 为圆心,
为圆心,![]() 为半径作圆.
为半径作圆.
综合运用
在你所作的图中,
(2)![]() 与⊙
与⊙![]() 的位置关系是 ;(直接写出答案)
的位置关系是 ;(直接写出答案)
(3)若![]() ,
,![]() ,求⊙
,求⊙![]() 的半径.
的半径.
(4)在(3)的条件下,求以![]() 为轴把△ABC旋转一周得到的圆锥的侧面积.
为轴把△ABC旋转一周得到的圆锥的侧面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com