
【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB,垂足为H,若CD=1,EH=3,求BE长.
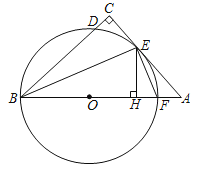
【答案】(1)详见解析;(2)![]()
【解析】
(1)连结OE,根据BE平分∠ABC,可得∠CBE=∠ABE,证明OE∥BC,进而可以证明AC是⊙O的切线;
(2)连结DE,根据BE平分∠ABC,AC⊥BC,EH⊥AB,可得CE=EH,再证明Rt△CDE≌△Rt△HFE,得CD=HF,利用勾股定理求出OE,再利用勾股定理即可求得BE的长.
解:(1)连结OE,
∵BE平分∠ABC,
∴∠CBE=∠ABE,
又∵OB=OE,
∴∠ABE=∠BEO,
∴∠CBE=∠BEO,
∴OE∥BC,
∵∠C=90°,即AC⊥BC,
∴OE⊥AC,
∴AC是⊙O的切线;
(2)连结DE,
∵BE平分∠ABC,AC⊥BC,EH⊥AB,
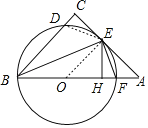
∴CE=EH,DE=EF,
∴Rt△CDE≌△Rt△HFE(HL),
∴CD=HF,
∵CD=1,
∴HF=1,
∵OE2=OH2+HE2,
∴OE2=(OE﹣1)2+32,
∴OE=5,
∴BH=9,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在坡角为33°的山坡上有一建筑物AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得建筑物AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求建筑物AB的高(AB,CD均与水平面垂直,参考数据:sin33°=0.54,cos33°=0.84,tan33°=0.65)
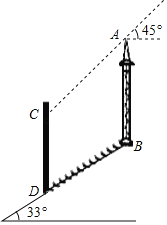
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王辉在某景区经营一个小摊位,他以10元/根的价格购进一批登山杖,经市场调查发现当售价为24元/根时,每天可出售156根,此后售价每增加5元,就会少售出30根.
(1)求登山杖的单根售价![]() (元)与销售数量
(元)与销售数量![]() (根)之间的函数关系式;
(根)之间的函数关系式;
(2)若设王辉每天的日销售利润为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)为了避免恶性竞争且保障商家获得一定利润,景区管理处规定登山杖的销售单价不得低于32元且不高于36元,则王辉的日销售利润最大是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC 内接于⊙O,过点 A 作⊙O 的切线交 CB 的延长线于点 P,且∠PAB=45°.
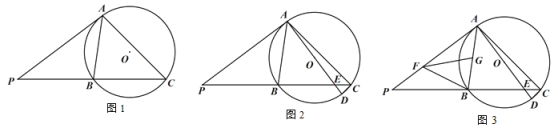
(1)如图 1,求∠ACB 的度数;
(2)如图 2,AD 是⊙O 的直径,AD 交 BC 于点 E,连接 CD,求证:AC CD ![]() ;
;
(3)如图 3 ,在(2)的条件下,当 BC 4![]() CD 时,点 F,G 分别在 AP,AB 上,连接 BF,FG,∠BFG=∠P,且 BF=FG,若 AE=15,求 FG 的长.
CD 时,点 F,G 分别在 AP,AB 上,连接 BF,FG,∠BFG=∠P,且 BF=FG,若 AE=15,求 FG 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点两点
经过点两点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线上一个动点,设点
是抛物线上一个动点,设点![]() 的横坐标为
的横坐标为![]() .连接
.连接![]()
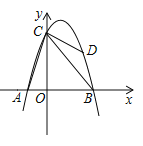
(1)求抛物线的函数表达式;
(2)当![]() 的面积等于
的面积等于![]() 的面积时,求
的面积时,求![]() 的值;
的值;
(3)当![]() 时,若点
时,若点![]() 是
是![]() 轴正半轴上上的一个动点,点
轴正半轴上上的一个动点,点![]() 是抛物线上动点,试判断是否存在这样的点
是抛物线上动点,试判断是否存在这样的点![]() ,使得以点
,使得以点![]() 为顶点的四边形是平行四边形.若存在,请直接写出点
为顶点的四边形是平行四边形.若存在,请直接写出点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抗击疫情,众志成城,举国上下,共克时艰.为确定应对疫情影响稳外贸稳外资的新举措,国务院总理李克强 3 月 10 日主持召开国务院常务会议,要求更好发挥专项再贷款再贴 现政策作用,支持疫情防控保供和企业纾困发展.会议指出,近段时间,有关部门按照国务 院要求,引导金融机构实施![]() 亿元专项再贷款政策,以优惠利率资金有力支持了疫情防 控物资保供、农业和企业特别是小微企业复工复产.要进一步把政策落到位,加快贷款投放 进度,更好保障防疫物资保供、春耕备耕、国际供应链产品生产、劳动密集型产业、中小微 企业等资金需求.数据
亿元专项再贷款政策,以优惠利率资金有力支持了疫情防 控物资保供、农业和企业特别是小微企业复工复产.要进一步把政策落到位,加快贷款投放 进度,更好保障防疫物资保供、春耕备耕、国际供应链产品生产、劳动密集型产业、中小微 企业等资金需求.数据![]() 亿元用科学记数法表示为( )
亿元用科学记数法表示为( )
A.![]() 元B.
元B.![]() 元C.
元C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究 如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 两点且与
两点且与![]() 轴的负半轴交于点
轴的负半轴交于点![]() .
.
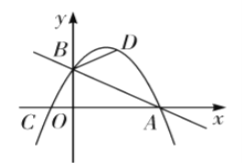
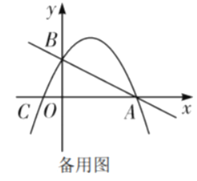
(1)求该抛物线的解析式;
(2)若![]() 为直线
为直线![]() 上方抛物线上的一个动点,当
上方抛物线上的一个动点,当![]() 时,求
时,求![]() 点的坐 标;
点的坐 标;
(3)已知![]() 分别是直线
分别是直线![]() 和抛物线上的动点,当以
和抛物线上的动点,当以![]() 为顶点的四边形 是平行四边形,且以
为顶点的四边形 是平行四边形,且以![]() 为边时,请直接写出所有符合条件的点
为边时,请直接写出所有符合条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018无锡市体育中考男生项目分为速度耐力类、力量类和灵巧类,每位考生只能在三类中各选一项进行考试.其中速度耐力类项目有:50米跑、800米跑、50米游泳;力量类项目有:掷实心球、引体向上;灵巧类项目有:30秒钟跳绳、立定跳远、俯卧撑、篮球运球.男生小明“50米跑”是强项,他决定必选,其它项目在平时测试中成绩完全相同,他决定随机选择.
(1)请用画树状图或列表的方法求“小明‘选50米跑、引体向上和立定跳远’”的概率;
(2)小明所选的项目中有立定跳远的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com