
如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线点F.问:
(1)图中△APD与哪个三角形全等?并说明理由;
(2)求证:△APE∽△FPA;
(3)猜想:线段PC,PE ,PF之间存在什么关系?并说明理由.
,PF之间存在什么关系?并说明理由.

 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:
如图,在△ABC中,AB=AC,∠A=30°,以B为圆心,BC的长为半径圆弧,交AC于点D,连接BD,则∠ABD=( )

A. 30° B.45° C.60° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
已知在矩形ABCD中,P是边AD上的一动点,联结BP、CP,过点B作射线交线段CP的延长线于点E,交边AD于点M,且使得∠ABE=∠CBP,如果AB=2,BC=5,AP=x,PM=y;
(1)求y关于x的函数解析式,并写出 它的定义域;
它的定义域;
(2)当AP=4时,求∠EBP的正切值;
(3)如果△EBC是以∠EBC为底角的等腰三角形,求AP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知∠MON=90°,A是∠MON内部的一点,过点A作AB⊥ON,垂足为点B,AB=3厘米,OB=4厘米,动点E,F同时从O点出发,点E以1.5厘米/秒的速度沿ON方向运动,点F以2厘米/秒的速度沿OM方向运动,EF与OA交于点C,连接AE,当点E到达点B时,点F随之停止运 动.设运动时间为t秒(t>0).
动.设运动时间为t秒(t>0).
(1)当t=1秒时,△EOF与△ABO是否相似?请说明理由;
(2)在运动过程中,不论t取何值时,总有EF⊥OA.为什么?
(3)连接AF,在运动过程中,是否存在某一时刻t,使得S△AEF=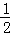 S四边形AEOF?若存在,请求出此时t的值;若不存在,请说明理由.
S四边形AEOF?若存在,请求出此时t的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为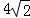 ,则a的值是( )
,则a的值是( )
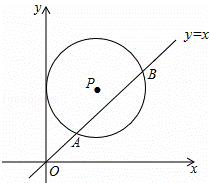
A. 4 B.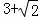 C.
C.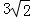 D.
D. 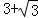
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com