
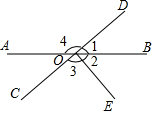
 如图,直线AB,CD相交于点O,且∠1=∠2,已知∠2:∠3=2:5,求∠4、∠AOC的度数.
如图,直线AB,CD相交于点O,且∠1=∠2,已知∠2:∠3=2:5,求∠4、∠AOC的度数. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 相等的两个角是对顶角 | |
| B. | 邻补角是互补的两个角,互补的两个角也是邻补角 | |
| C. | 如果两个角有公共顶点和一条公共边,那么它们互为邻补角 | |
| D. | 两条直线相交,如果它们所成的邻补角相等,那么一对对顶角也互补 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
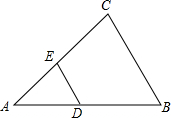 如图,在△ABC中,已知DE∥BC,$\frac{AE}{EC}$=$\frac{2}{3}$,则△ADE与△ABC的周长之比为( )
如图,在△ABC中,已知DE∥BC,$\frac{AE}{EC}$=$\frac{2}{3}$,则△ADE与△ABC的周长之比为( )| A. | 2:3 | B. | 3:2 | C. | 2:5 | D. | 4:25 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源:2017届江苏省无锡市九年级下学期第一次模拟考试数学试卷(解析版) 题型:解答题
已知:在平面直角坐标系中,抛物线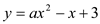 (
(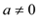 )交x轴于A、B两点,交y轴于点C,且对称轴为直线x=―2 .
)交x轴于A、B两点,交y轴于点C,且对称轴为直线x=―2 .
(1)求该抛物线的解析式及顶点D的坐标;
(2)若点P(0,t)是y轴上的一个动点,请进行如下探究:
探究一:如图1,设△PAD的面积为S,令W=t·S,当0<t<4时,W是否有最大值?如果有,求出W的最大值和此时t的值;如果没有,说明理由;
探究二:如图2,是否存在以P、A、D为顶点的三角形与Rt△AOC相似?如果存在,求点P的坐标;如果不存在,请说明理由.
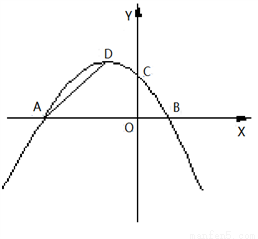
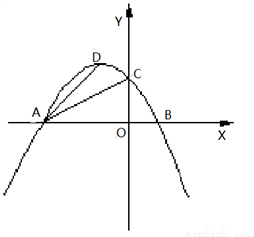
图1 图2
查看答案和解析>>
科目:初中数学 来源:2016-2017学年北京市西城区七年级上学期期末考试数学试卷(解析版) 题型:填空题
观察下面的图形(每个正方形的边长均为1)和相应的等式,探究其中的规律:
①
 1×
1× =1-
=1-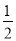
②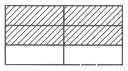
 2×
2×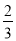 =2-
=2-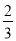
③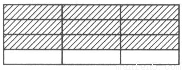
 3×
3×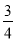 =3-
=3-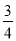
……
(1)在下面给出的四个正方形中画出第四个图形,并在右边写出与之对应的等式;

 _______________
_______________
(2)猜想并写出与第几个图形相对应的等式:______________________________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com