
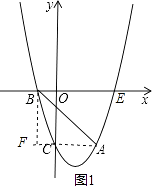
【题目】如图,抛物线y=ax2+bx﹣3经过点A(2,﹣3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.
(1)求抛物线的解析式;
(2)点D在y轴上,且∠BDO=∠BAC,求点D的坐标;
(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.
【答案】
(1)
解:由y=ax2+bx﹣3得C(0.﹣3),
∴OC=3,
∵OC=3OB,
∴OB=1,
∴B(﹣1,0),
把A(2,﹣3),B(﹣1,0)代入y=ax2+bx﹣3得 ![]() ,
,
∴ ![]() ,
,
∴抛物线的解析式为y=x2﹣2x﹣3
(2)
解:设连接AC,作BF⊥AC交AC的延长线于F,
∵A(2,﹣3),C(0,﹣3),
∴AF∥x轴,
∴F(﹣1,﹣3),
∴BF=3,AF=3,
∴∠BAC=45°,
设D(0,m),则OD=|m|,
∵∠BDO=∠BAC,
∴∠BDO=45°,
∴OD=OB=1,
∴|m|=1,
∴m=±1,
∴D1(0,1),D2(0,﹣1)
(3)
解:设M(a,a2﹣2a﹣3),N(1,n),
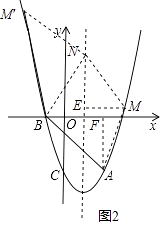
①以AB为边,则AB∥MN,AB=MN,如图2,过M作ME⊥对称轴y于E,AF⊥x轴于F,
则△ABF≌△NME,
∴NE=AF=3,ME=BF=3,
∴|a﹣1|=3,
∴a=3或a=﹣2,
∴M(4,5)或(﹣2,11);
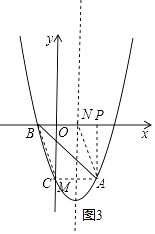
②以AB为对角线,BN=AM,BN∥AM,如图3,
则N在x轴上,M与C重合,
∴M(0,﹣3),
综上所述,存在以点A,B,M,N为顶点的四边形是平行四边形,M(4,5)或(﹣2,11)或(0,﹣3).
【解析】(1)待定系数法即可得到结论;(2)连接AC,作BF⊥AC交AC的延长线于F,根据已知条件得到AF∥x轴,得到F(﹣1,﹣3),设D(0,m),则OD=|m|即可得到结论;(3)设M(a,a2﹣2a﹣3),N(1,n),①以AB为边,则AB∥MN,AB=MN,如图2,过M作ME⊥对称轴y于E,AF⊥x轴于F,于是得到△ABF≌△NME,证得NE=AF=3,ME=BF=3,得到M(4,5)或(﹣2,11);②以AB为对角线,BN=AM,BN∥AM,如图3,则N在x轴上,M与C重合,于是得到结论.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


科目:初中数学 来源: 题型:
【题目】甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示,当乙到达终点A时,甲还需分钟到达终点B. 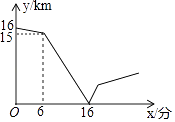
查看答案和解析>>
科目:初中数学 来源: 题型:
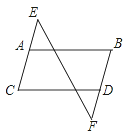
【题目】如图,有以下3句话:①AB∥CD,②∠B=∠C、③∠E=∠F、请以其中2句话为条件,第三句话为结论构造命题.
(1)你构造的是哪几个命题?
(2)你构造的命题是真命题还是假命题?请加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下统计图表: 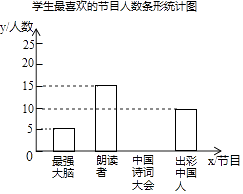
学生最喜爱的节目人数统计表
节目 | 人数(名) | 百分比 |
最强大脑 | 5 | 10% |
朗读者 | 15 | b% |
中国诗词大会 | a | 40% |
出彩中国人 | 10 | 20% |
根据以上提供的信息,解答下列问题:
(1)x= , a= , b=;
(2)补全上面的条形统计图;
(3)若该校共有学生1000名,根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
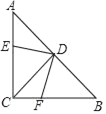
【题目】如图,已知在△ABC中,∠ACB=90°,AC=BC,D为AB中点,点E,F分别在AC,BC边上,且AE=CF.
(1)求证:DE=DF;
(2)连接EF,求∠DEF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2015次运动后,动点P的坐标是( )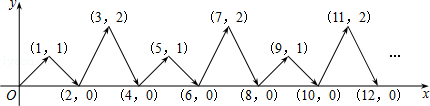
A.(2015,0)
B.(2015,1)
C.(2015,2)
D.(2016,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店购进一批甲、乙两种款型时尚T恤衫,甲种款型共用了7800元,乙种款型共用了6400元,甲种款型的件数是乙种款型件数的1.5倍,甲种款型每件的进价比乙种款型每件的进价少30元.
(1)甲、乙两种款型的T恤衫各购进多少件?
(2)商店进价提高60%标价销售,销售一段时间后,甲款型全部售完,乙款型剩余一半,商店决定对乙款型按标价的五折降价销售,很快全部售完,求售完这批T恤衫商店共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 边长为
边长为![]() 的等边三角形
的等边三角形![]() 的顶点
的顶点![]() 分别在边
分别在边![]() ,
,![]() 上当
上当![]() 在边
在边![]() 上运动时,
上运动时,![]() 随之在边
随之在边![]() 上运动,等边三角形的形状保持不变,运动过程中,点
上运动,等边三角形的形状保持不变,运动过程中,点![]() 到点
到点![]() 的最大距离为( )
的最大距离为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)是一次函数关系,如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,每月在收取5500元的基础上,超过部分每平方米收取4元.

(1)求如图所示的y与x的函数解析式;(不要求写取值范围)
(2)如果某学校目前的绿化面积是1200平方米.试通过计算说明:选择哪家公司的服务,每月的绿化养护费用较少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com