练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    有一直径为1m的圆形铁皮，要从中剪出一个最大圆心角是的扇形ABC求：

    (1)被剪阴影部分的面积．

    (2)用留的扇形铁皮围成一个圆锥，该圆锥的底面圆的半径是多少？

    答案：
    解析：

    　　(1)连接BC．

    　　∵∠BAC＝，∴BC是直径．

    　　在Rt△ABC中，AB2＋AC2＝BC2，

    　　AB＝．

    　　S阴影＝S⊙O－S扇形ABC＝π·()2－＝(m2)．

    　　(2)设圆锥底面圆的半径为r m，则

    　　2πr＝．

    　　r＝．

    　　答：被剪阴影部分的面积为m2；圆锥的底面圆的半径m．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

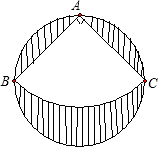    精英家教网如图，有一直径为1m的圆形铁皮，要从中剪出一个最大的圆心角是90°的扇形ABC
    （1）找到圆形铁皮的圆心O（要求尺规作图，保留作图痕迹）；
    （2）求剪掉部分即阴影部分的面积（结果保留π）；
    （3）用所留的扇形铁皮围成一个圆锥，该圆锥的底面半径是多少？

    查看答案和解析>>

    科目：初中数学 来源：数学教研室 题型：044

    如图所示，有一直径为1m的圆形铁皮，要从中剪出一个最大的圆心角是90°的扇形ABC．

    (1)求被剪掉阴影部分的面积；

    (2)用所留的扇形铁皮围成一个圆锥，则该圆锥的底面圆的半径是多少？(结果可用根号)

    查看答案和解析>>

    科目：初中数学 来源：数学教研室 题型：059

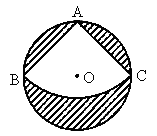
    如图所示，有一直径为1m的圆形铁皮，要从中剪出一个最大的圆心角是90°的扇形BAC．求：

    (1)被剪掉阴影部分的面积；

    (2)用剪下的扇形铁皮围成一个圆锥，该圆锥的底面圆半径是多少？(结果可保留根号)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图所示，有一直径是1m的圆形铁皮，要从中剪出一个圆心角为90°的扇形ABC。

       （1）求被剪掉的阴影部分的面积；

       （2）用所剪的扇形铁皮围成一个圆锥，该圆锥的底面半径是多少？（结果可用根号表示）

    查看答案和解析>>

    同步练习册答案