
【题目】已知常数p>0,数列{an}满足an+1=|p﹣an|+2an+p,n∈N*.
(1)若a1=﹣1,p=1, ①求a4的值;
②求数列{an}的前n项和Sn;
(2)若数列{an}中存在三项ar , as , at(r,s,t∈N*,r<s<t)依次成等差数列,求 ![]() 的取值范围.
的取值范围.
【答案】
(1)解:①∵an+1=|p﹣an|+2an+p,
∴a2=|1﹣a1|+2a1+1=2﹣2+1=1,
a3=|1﹣a2|+2a2+1=0+2+1=3,
a4=|1﹣a3|+2a3+1=2+6+1=9,
②∵a2=1,an+1=|1﹣an|+2an+1,
∴当n≥2时,an≥1,
当n≥2时,an+1=﹣1+an+2an+1=3an,即从第二项起,数列{an}是以1为首项,以3为公比的等比数列,
∴数列{an}的前n项和Sn=a1+a2+a3+a4+…+an=﹣1+ ![]() =
= ![]() ﹣
﹣ ![]() ,(n≥2),
,(n≥2),
显然当n=1时,上式也成立,
∴Sn= ![]() ﹣
﹣ ![]()
(2)解:∵an+1﹣an=|p﹣an|+an+p≥p﹣an+an+p=2p>0,
∴an+1>an,即{an}单调递增.
(i)当 ![]() ≥1时,有a1≥p,于是an≥a1≥p,
≥1时,有a1≥p,于是an≥a1≥p,
∴an+1=|p﹣an|+2an+p=an﹣p+2an+p=3an,∴ ![]() .
.
若数列{an}中存在三项ar,as,at(r,s,t∈N*,r<s<t)依次成等差数列,则有2as=ar+at,
即2×3s﹣1=3r﹣1+3t﹣1.(*)
∵s≤t﹣1,∴2×3s﹣1= ![]() <3t﹣1<3r﹣1+3t﹣1.因此(*)不成立.因此此时数列{an}中不存在三项ar,as,at(r,s,t∈N*,r<s<t)依次成等差数列.
<3t﹣1<3r﹣1+3t﹣1.因此(*)不成立.因此此时数列{an}中不存在三项ar,as,at(r,s,t∈N*,r<s<t)依次成等差数列.
(ii)当 ![]() 时,有﹣p<a1<p.此时a2=|P﹣a1|+2a1+p=p﹣a1+2a1+p=a1+2p>p.
时,有﹣p<a1<p.此时a2=|P﹣a1|+2a1+p=p﹣a1+2a1+p=a1+2p>p.
于是当n≥2时,an≥a2>p.从而an+1=|p﹣an|+2an+p=an﹣p+2an+p=3an.∴an=3n﹣2a2=3n﹣2(a1+2p)(n≥2).
若数列{an}中存在三项ar,as,at(r,s,t∈N*,r<s<t)依次成等差数列,则有2as=ar+at,
同(i)可知:r=1.于是有2×3s﹣2(a1+2p)=a1+3t﹣2(a1+2p),∵2≤S≤t﹣1,∴ ![]() =2×3s﹣2﹣3t﹣2=
=2×3s﹣2﹣3t﹣2= ![]() ﹣
﹣ ![]() <0.∵2×3s﹣2﹣3t﹣2是整数,∴
<0.∵2×3s﹣2﹣3t﹣2是整数,∴ ![]() ≤﹣1.于是a1≤﹣a1﹣2p,即a1≤﹣p.与﹣p<a1<p矛盾.
≤﹣1.于是a1≤﹣a1﹣2p,即a1≤﹣p.与﹣p<a1<p矛盾.
故此时数列{an}中不存在三项ar,as,at(r,s,t∈N*,r<s<t)依次成等差数列.
(iii)当 ![]() ≤﹣1时,有a1≤﹣p<p.a1+p≤0.
≤﹣1时,有a1≤﹣p<p.a1+p≤0.
于是a2=|P﹣a1|+2a1+p=p﹣a1+2a1+p=a1+2p.
a3=|p﹣a2|+2a2+p=|a1+p|+2a1+5p.=﹣a1﹣p+2a1+5p=a1+4p.
此时数列{an}中存在三项a1,a2,a3依次成等差数列.
综上可得: ![]() ≤﹣1
≤﹣1
【解析】(1)①an+1=|p﹣an|+2an+p,可得a2=|1﹣a1|+2a1+1=2﹣2+1=1,同理可得a3=3,a4=9.②a2=1,an+1=|1﹣an|+2an+1,当n≥2时,an≥1,当n≥2时,an+1=﹣1+an+2an+1=3an , 即从第二项起,数列{an}是以1为首项,以3为公比的等比数列,利用等比数列的求和公式即可得出Sn . (2)an+1﹣an=|p﹣an|+an+p≥p﹣an+an+p=2p>0,可得an+1>an , 即{an}单调递增.(i)当 ![]() ≥1时,有a1≥p,于是an≥a1≥p,可得an+1=|p﹣an|+2an+p=an﹣p+2an+p=3an ,
≥1时,有a1≥p,于是an≥a1≥p,可得an+1=|p﹣an|+2an+p=an﹣p+2an+p=3an , ![]() .利用反证法即可得出不存在.(ii)当
.利用反证法即可得出不存在.(ii)当 ![]() 时,有﹣p<a1<p.此时a2=|P﹣a1|+2a1+p=p﹣a1+2a1+p=a1+2p>p.于是当n≥2时,an≥a2>p.从而an+1=|p﹣an|+2an+p=an﹣p+2an+p=3an . an=3n﹣2a2=3n﹣2(a1+2p)(n≥2).假设存在2as=ar+at , 同(i)可知:r=1.得出矛盾,因此不存在.(iii)当
时,有﹣p<a1<p.此时a2=|P﹣a1|+2a1+p=p﹣a1+2a1+p=a1+2p>p.于是当n≥2时,an≥a2>p.从而an+1=|p﹣an|+2an+p=an﹣p+2an+p=3an . an=3n﹣2a2=3n﹣2(a1+2p)(n≥2).假设存在2as=ar+at , 同(i)可知:r=1.得出矛盾,因此不存在.(iii)当 ![]() ≤﹣1时,有a1≤﹣p<p.a1+p≤0.于是a2=|P﹣a1|+2a1+p=p﹣a1+2a1+p=a1+2p.a3=a1+4p.即可得出结论.
≤﹣1时,有a1≤﹣p<p.a1+p≤0.于是a2=|P﹣a1|+2a1+p=p﹣a1+2a1+p=a1+2p.a3=a1+4p.即可得出结论.
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】设△ABC的一边长为x,这条边上的高为y,y与x满足的反比例函数关系如图所示.当△ABC为等腰直角三角形时,x+y的值为( ) 
A.4
B.5
C.5或3 ![]()
D.4或3 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,设∠A、∠B、∠C的对边分别为a,b,c,过点A作AD⊥BC,垂足为D,会有sin∠C= ![]() ,则
,则
S△ABC= ![]() BC×AD=
BC×AD= ![]() ×BC×ACsin∠C=
×BC×ACsin∠C= ![]() absin∠C,
absin∠C,
即S△ABC= ![]() absin∠C
absin∠C
同理S△ABC= ![]() bcsin∠A
bcsin∠A
S△ABC= ![]() acsin∠B
acsin∠B
通过推理还可以得到另一个表达三角形边角关系的定理﹣余弦定理:
如图2,在△ABC中,若∠A、∠B、∠C的对边分别为a,b,c,则
a2=b2+c2﹣2bccos∠A
b2=a2+c2﹣2accos∠B
c2=a2+b2﹣2abcos∠C
用上面的三角形面积公式和余弦定理解决问题:
(1)如图3,在△DEF中,∠F=60°,∠D、∠E的对边分别是3和8.求S△DEF和DE2 . 
解:S△DEF= ![]() EF×DFsin∠F=;
EF×DFsin∠F=;
DE2=EF2+DF2﹣2EF×DFcos∠F= .
(2)如图4,在△ABC中,已知AC>BC,∠C=60°,△ABC'、△BCA'、△ACB'分别是以AB、BC、AC为边长的等边三角形,设△ABC、△ABC'、△BCA'、△ACB'的面积分别为S1、S2、S3、S4 , 求证:S1+S2=S3+S4 . 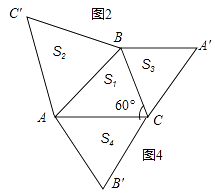
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次世界魔方大赛吸引世界各地共600名魔方爱好者参加,本次大赛首轮进行3×3阶魔方赛,组委会随机将爱好者平均分到20个区域,每个区域30名同时进行比赛,完成时间小于8秒的爱好者进入下一轮角逐;如图是3×3阶魔方赛A区域30名爱好者完成时间统计图,求: ①A区域3×3阶魔方爱好者进入下一轮角逐的人数的比例(结果用最简分数表示).
②若3×3阶魔方赛各个区域的情况大体一致,则根据A区域的统计结果估计在3×3阶魔方赛后进入下一轮角逐的人数.
③若3×3阶魔方赛A区域爱好者完成时间的平均值为8.8秒,求该项目赛该区域完成时间为8秒的爱好者的概率(结果用最简分数表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E. 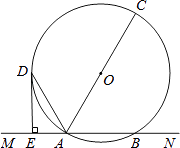
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
(3)在(2)的条件下,直接写出tan∠CAB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,花丛中有一路灯杆AB.在灯光下,小明在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时小明的影长GH=5米.如果小明的身高为1.7米,求路灯杆AB的高度(精确到0.1米). 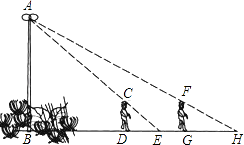
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的方程x2﹣(m+2)x+m+1=0.
(1)求证:该方程总有实数根;
(2)若二次函数y=x2﹣(m+2)x+m+1(m>0)与x轴交点为A,B(点A在点B的左边),且两交点间的距离是2,求二次函数的表达式;
(3)横、纵坐标都是整数的点叫做整点.
在(2)的条件下,垂直于y轴的直线y=n与抛物线交于点E,F.若抛物线在点E,F之间的部分与线段EF所围成的区域内(包括边界)恰有7个整点,结合函数的图象,直接写出n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com