
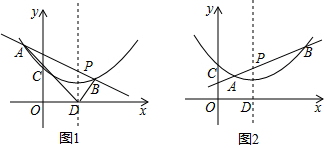
分析 (1)先确定出抛物线的对称轴,即可确定出点P的坐标;
(2)先判断出AE=AP,同理BP=BF,进而判定出△AED∽△BFD即可得出结论;
(3)先求出EG=FH=OC=1,再判断出△PAG∽△PBH即可得出结论.
解答 解:(1)∵抛物线y=$\frac{1}{2}$x2-x+1,
∴抛物线的对称轴为x=1,
∵抛物线的对称轴交x轴于点D,交直线AB(y=kx-k+1)于点P.
∴当x=1时,y=1,
∴P(1,1);
(2)如图1,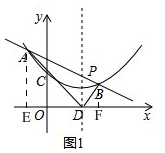 分别过点A,B作x轴的垂线,垂足为E,F,设A(x1,y1),B(x2,y2),
分别过点A,B作x轴的垂线,垂足为E,F,设A(x1,y1),B(x2,y2),
∴y1=$\frac{1}{2}$x12-x1+1=$\frac{1}{2}$(x1-1)2+$\frac{1}{2}$,
∴2y1-1=(x1-1)2,
∴AP2=(y1-1)2+(x1-1)2=(y1-1)2+2y1=y12,
∴AE=AP,
同理:BP=BF,
∴$\frac{AP}{BP}=\frac{ED}{FD}=\frac{AE}{BF}$,
∵∠AED=∠BFD,
∴△AED∽△BFD,
∴∠ADE=∠BDF,
∴∠ADP=∠BDP,
∴△ABD的内心在射线DP上;
(3)如图2,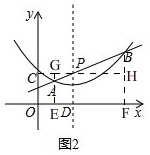 分别过点A,B作x轴的垂线,垂足为E,F,连接CP并延长交BF于H,交EA延长线于G,
分别过点A,B作x轴的垂线,垂足为E,F,连接CP并延长交BF于H,交EA延长线于G,
易证四边形COEG是矩形,
∵P(1,1),C(0,1),
∴OC=1,
∴EG=FH=OC=1,
易证△PAG∽△PBH,
∴$\frac{AG}{AP}=\frac{BH}{BP}$,
由(2)知,AE=AP,BP=BF,
∴$\frac{1-AP}{AP}=\frac{BP-1}{BP}$,
∴$\frac{1}{AP}+\frac{1}{BP}$=2.
点评 此题是二次函数综合题,主要考查了待定系数法,相似三角形的判定和性质,解(2)的关键是判断出AE=AP,解(3)的关键是求出EG=1,是一道中等难度的中考常考题.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:选择题
| A. | ①②③④ | B. | ①②④ | C. | ①②③ | D. | ①② |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
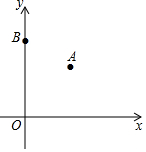 如图,在平面直角坐标系中,已知点A(3,3),B(0,5),若在坐标轴上找一点C,使得△ABC是等腰三角形,则这样的点C有( )
如图,在平面直角坐标系中,已知点A(3,3),B(0,5),若在坐标轴上找一点C,使得△ABC是等腰三角形,则这样的点C有( )| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
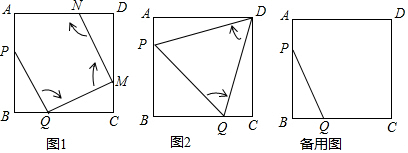
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
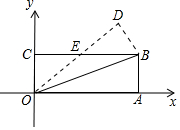 如图,在平面直角坐标系xOy中,O为坐标系原点,A(3,0),B(3,1),C(0,1),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则OD所在直线的解析式为( )
如图,在平面直角坐标系xOy中,O为坐标系原点,A(3,0),B(3,1),C(0,1),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则OD所在直线的解析式为( )| A. | $y=\frac{4}{5}x$ | B. | $y=\frac{5}{4}x$ | C. | $y=\frac{3}{4}x$ | D. | $y=\frac{4}{3}x$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
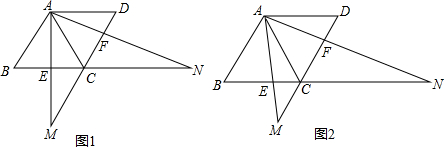
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com