
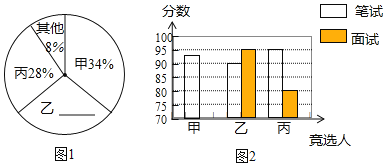
����Ŀ��ɽ��ʡʵ����ѧ�����廪��ѧ�Ƽ�һ��ѧ�������ݹ涨���Ƽ����������ɱ��꼶200��ѧ������ͶƱ��ÿ��ֻ���Ƽ�һ�ˣ�������ȨƱ����ѡ����Ʊ�����ļס��ҡ������ˣ�ͶƱ���ͳ����ͼ1��
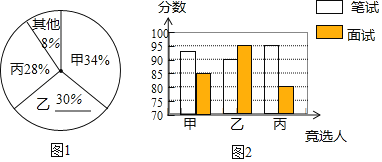
��Σ���������ѡ�˽����˱��Ժ�����������ԣ�����ɼ������ʾ��
������Ŀ | ���Գɼ�/�� | ||
�� | �� | �� | |
���� | 92 | 90 | 95 |
���� | 85 | 95 | 80 |
ͼ2��ijͬѧ�����ϱ����Ƶ�һ������ȫ������ͼ���������������Ϣ����������⣺
��1����ȫͼ1��ͼ2��
��2�������ÿ����ѡ�˵ĵ�Ʊ����
��3����ÿ����ѡ�˵�һƱ��1�֣�ͶƱ�����ԡ���������÷ְ���2��5��3�ı�ȷ��������������ѡ�˵�ƽ���ɼ����ɼ��ߵĽ���¼ȡ��Ӧ��¼ȡ˭��
��4����ѧУ��������������ѡ�������ѡ�����μ��廪��ѧ����Ӫ������ұ�ѡ�еĸ��ʣ���Ҫ���б�����״ͼ��
���𰸡���1���𰸼��⣻��2���ף�68���ң�60������56����3��Ӧ��¼ȡ�ң���4��![]() .
.
��������
��1������ͳ��ͼ����1��ȥ�ף�����������ռ�İٷֱȼ�Ϊ����ռ�İٷֱȣ�Ȼ����ݱ����֪�����Գɼ�Ϊ85����ȫ����ͳ��ͼ���ɣ�
��2���ֱ�������200���Ը�����ռ�İٷֱȼ��������Ʊ����
��3�����ռ�Ȩƽ�����ļ��㷽���ֱ������ף��ң�����ƽ���֣�Ȼ�����ѡ��ƽ���ָߵ�¼ȡ��
��4������״ͼ�г����еĿ����ԣ������ҳ����ұ�ѡ�еĿ��ܣ����ø��ʹ�ʽ���㼴��.
�⣺��1��ͼ1���ҵİٷֱȣ�1��8%��28%��34%��30%��
ͼ2�У������Եijɼ�Ϊ85�֣�
��ͼ��
��2����Ʊ���ǣ�200��34%��68��Ʊ����
�ҵ�Ʊ���ǣ�200��30%��60��Ʊ����
����Ʊ���ǣ�200��28%��56��Ʊ����
��3����ƽ���ɼ���![]() ���֣�
���֣�
�ҵ�ƽ���ɼ���![]() ���֣�
���֣�
����ƽ���ɼ���![]() ���֣�
���֣�
���ҵ�ƽ���ɼ���ߣ�
��Ӧ��¼ȡ�ң�
��4������״ͼΪ��
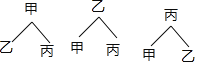
����6�ֵȿ��ܵĽ���������м��ұ�ѡ�еĽ����Ϊ2��
���Լ��ұ�ѡ�еĸ��ʣ�![]()


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�͡�CDE���Ե�CΪ������������������Σ�

��1����ͼ1����AB��AC��CD��CE����BAC����DCE��90��ʱ������BD��ȡBD���е�M������AM��̽��AM��BE֮���������ϵ����֤����Ľ��ۣ�
��2����ͼ2����AB��AC����BAC��120�㣬��CDE��60�㣬��DCE��90��ʱ������BD��ȡBD���е�M������AM��̽��AM��BE֮��Ĺ�ϵ����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P������ABCD�ĶԽ���BD��һ�㣬����CP���ӳ�����AD��E����BA���ӳ����ڵ�F.
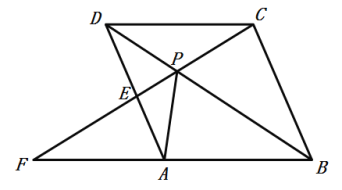
��1����֤��![]() .
.
��2�����![]() �����߶�PC�ij�.
�����߶�PC�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l1��y=kx+b ������A����![]() ��0���͵�B��2��5����
��0���͵�B��2��5����
��1����ֱ��l1��y��Ľ������ꣻ
��2������C��a��a+2�����D��ֱ��l1�ϣ�����D��ֱ��l2��x�������ύ�ڵ� E����AC=CD=CE ʱ����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y����![]() x2+bx+c��x�ύ��A��B���㣬��y�ύ��C��ֱ��y��
x2+bx+c��x�ύ��A��B���㣬��y�ύ��C��ֱ��y��![]() x+3������A��C��
x+3������A��C��
��1���������ߵĽ���ʽ��
��2��P����������һ���㣬��P��PM��y�ύֱ��AC�ڵ�M�����P�ĺ�����Ϊt��
�����Ե�C��O��M��PΪ������ı�����ƽ���ı��Σ���t��ֵ��
�ڵ�����MP��AC��MO��һ������ƽ�������������ߵļн�ʱ��ֱ��д��t��ֵ��
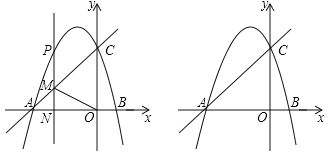
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ͼ�ζ��������Ϊ1�������ΰ�һ���Ĺ�����ɣ����У��ڣ�1����ͼ�������Ϊ1����������2�����ڣ�2����ͼ�������Ϊ1����������5�����ڣ�3����ͼ�������Ϊ1����������9�������˹��ɣ���ڣ�6����ͼ�������Ϊ1�������εĸ���Ϊ��������

A.14B.20C.24D.27
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����λ��t��![]() ������a��b��c��ȫ����Ҷ���Ϊ0�����������и���λ�ϵ����ֱؿɵõ�һ���������һ����С���������������С���IJ����ԭ���IJ�������ΪT��t�������磬539�IJ���T��539����953��359��594��
������a��b��c��ȫ����Ҷ���Ϊ0�����������и���λ�ϵ����ֱؿɵõ�һ���������һ����С���������������С���IJ����ԭ���IJ�������ΪT��t�������磬539�IJ���T��539����953��359��594��
��1���������Ϸ������T��268������ ����T��513������ ����
��2����֪��λ��![]() ������a��b��1���IJ���T��
������a��b��1���IJ���T��![]() ����495���Ҹ���λ�ϵ�����֮��Ϊ3�ı����������з�����������λ����ֵ��
����495���Ҹ���λ�ϵ�����֮��Ϊ3�ı����������з�����������λ����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ĵ�����װ�к졢��������ɫ��С����Щ�����ɫ�ⶼ��ͬ�����к�����1�����������������һ����������ǰ���ĸ���Ϊ![]() ��
��
��1��������а���ĸ���������ͨ����ʽ���з��̽��
��2���������һ����Żز����ȣ����������һ���������ζ�������ͬ��ɫ��С��ĸ��ʣ���������״ͼ���б����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������Ʒ�̳�Ԥ��ijƷ���˶����ܹ�����������32000Ԫ������һ�������˶��������к�ܿ��������̳�����68000Ԫ�����ڶ��������˶��������������ǵ�һ������������2������ÿ���۶���10Ԫ��
��1�����̳����ι����������˶��������ף�
��2������������˶���ÿ���ۼ���ͬ����ȫ���������������20%����ôÿ���ۼ������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com