
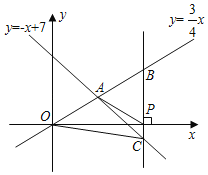
【题目】如图,在平面直角坐标系xOy中,已知正比例函数y=![]() x与一次函数y=﹣x+7的图象交于点A,x轴上有一点P(a,0).
x与一次函数y=﹣x+7的图象交于点A,x轴上有一点P(a,0).
(1)求点A的坐标;
(2)若△OAP为等腰三角形,则a= ;
(3)过点P作x轴的垂线(垂线位于点A的右侧)、分别交y=![]() x和y=﹣x+7的图象于点B、C,连接OC.若BC=
x和y=﹣x+7的图象于点B、C,连接OC.若BC=![]() OA,求△OBC的面积.
OA,求△OBC的面积.
【答案】(1)A(4,3);(2)±5或8或![]() ;(3)28
;(3)28
【解析】
(1)点A是两直线的交点,其坐标即方程组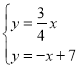 的解;
的解;
(2)分OA=PO、OA=AP、AP=OP适中情况,分别求解即可;
(3)P(a,0),则分别用含a的式子表示出B、C的坐标,从而表示出BC的长度,用勾股定理求得OA,然后根据BC=![]() OA求出a的值,从而利用三角形面积公式求解.
OA求出a的值,从而利用三角形面积公式求解.
解:(1)由题意: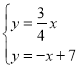 解得:
解得:![]() ,
,
故点A(4,3);
(2)点A(4,3),则OA=![]() ,
,
①当OA=PO=P1O时,
此时OA=5=PO=P1O,即a=±5

②当OA=AP时,如图,过点A做AM⊥x轴于点M
此时OM=MP=4
∴OP=8
则点P(8,0),即a=8;
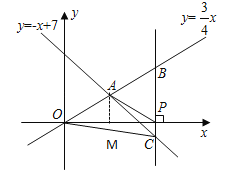
③当AP=OP时,如图所示,连接AP,过点A作AH⊥x轴于点H,
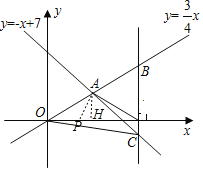
AP=PO=a,则PH=4﹣a,则(4﹣a)2+9=a2,
解得:a=![]() ;
;
综上,a=±5或8或![]() ;
;
故答案为:±5或8或![]() ;
;
(3)∵P(a,0),则点B、C的坐标分别为:(a,![]() a)、(a,﹣a+7),
a)、(a,﹣a+7),
∴BC=![]() a-(-a+7)=
a-(-a+7)=![]() a+a﹣7=
a+a﹣7=![]()
又∵BC=![]() OA且OA=
OA且OA=![]()
∴![]() =
=![]() ×5=7,
×5=7,
解得:a=8,
故点P(8,0),即OP=8;
△OBC的面积=![]() ×BC×OP=
×BC×OP=![]() ×7×8=28.
×7×8=28.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是△ABC的高线,CE是△ABC的角平分线,它们相交于点P.
(1)若∠B=40°,∠AEC=75°,求证:AB=BC;
(2)若∠BAC=90°,AP为△AEC边EC上中线,求∠B的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队计划修建一条长15千米的乡村公路,已知甲工程队每天比乙工程队每天多修路0.5千米,乙工程队单独完成修路任务所需天数是甲工程队单独完成修路任务所需天数的1.5倍.
(1)求甲、乙两个工程队每天各修路多少千米?
(2)若甲工程队每天的修路费用为0.5万元,乙工程队每天的修路费用为0.4万元,要使两个工程队修路总费用不超过5.2万元,甲工程队至少修路多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
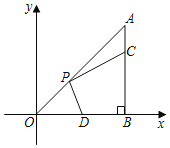
【题目】如图,在Rt△ABO中,∠OBA=90°,A(8,8),点C在边AB上,且![]() ,点D为OB的中点,点P为边OA上的动点,当点P在OA上移动时,使四边形PDBC周长最小的点P的坐标为( )
,点D为OB的中点,点P为边OA上的动点,当点P在OA上移动时,使四边形PDBC周长最小的点P的坐标为( )
A.(2,2)B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知:点A(0,0),B(![]() ,0),C(0,1).在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,则第n个等边三角形的边长等于( )
,0),C(0,1).在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,则第n个等边三角形的边长等于( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
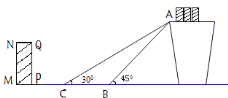
【题目】(本题满分8分)如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB长为4米.
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物MNQP是否需要挪走,并说明理由.(说明:⑴⑵的计算结果精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24,
≈2.24,![]() ≈2.45)
≈2.45)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( )
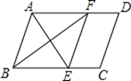
A. 13B. 14C. 15D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电动自行车已成为市民日常出行的首选工具。据某市品牌电动自行车经销商1至3月份统计,该品牌电动自行车1月份销售150辆,3月销售216辆.
(1)求该品牌电动车销售量的月平均增长率;
(2)若该品牌电动自行车的进价为2300元,售价2800元,则该经销商1月至3月共盈利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com