
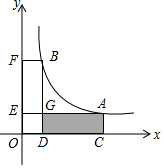
 如图,A(a,b)、B(1,4)(a>1)是反比例函数y=$\frac{k}{x}$(x>0)图象上两点,过A、B分别作x轴、y轴的垂线,垂足分别为C、D、E、F,AE、BD交于点G.则四边形ACDG的面积随着a的增大而增大.(填“减小”、“不变”或“增大”)
如图,A(a,b)、B(1,4)(a>1)是反比例函数y=$\frac{k}{x}$(x>0)图象上两点,过A、B分别作x轴、y轴的垂线,垂足分别为C、D、E、F,AE、BD交于点G.则四边形ACDG的面积随着a的增大而增大.(填“减小”、“不变”或“增大”) 分析 根据A(a,b)、B(1,4)(a>1)是反比例函数y=$\frac{k}{x}$(x>0)图象上两点,得出k=ab=1×4=4,b=$\frac{4}{a}$.再根据矩形ACDG的面积=矩形ACOE的面积-矩形ODGE的面积,得出四边形ACDG的面积=4-$\frac{4}{a}$,进而求解即可.
解答 解:∵A(a,b)、B(1,4)(a>1)是反比例函数y=$\frac{k}{x}$(x>0)图象上两点,
∴k=ab=1×4=4,
∴b=$\frac{4}{a}$.
∵过A、B分别作x轴、y轴的垂线,垂足分别为C、D、E、F,AE、BD交于点G,
∴四边形ACDG是矩形,
∴矩形ACDG的面积=矩形ACOE的面积-矩形ODGE的面积
=ab-1•b
=4-$\frac{4}{a}$,
∵a增大时,$\frac{4}{a}$减小,4-$\frac{4}{a}$增大,
∴四边形ACDG的面积随着a的增大而增大.
故答案为增大.
点评 本题考查了反比例函数中比例系数k的几何意义,反比例函数图象上点的坐标特征,矩形的面积,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
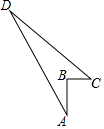 如图,四边形ABCD中,AB=4cm,BC=3cm,CD=12cm,DA=13cm,且∠ABC=90°,则四边形ABCD的面积为( )
如图,四边形ABCD中,AB=4cm,BC=3cm,CD=12cm,DA=13cm,且∠ABC=90°,则四边形ABCD的面积为( )| A. | 6cm2 | B. | 30cm2 | C. | 24cm2 | D. | 36cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
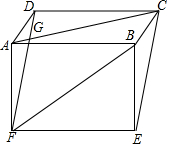 已知:如图,在平行四边形ABCD和矩形ABEF中,AC与DF相交于点G.
已知:如图,在平行四边形ABCD和矩形ABEF中,AC与DF相交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
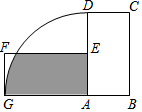 如图,将矩形ABCD绕点A逆时针旋转90°至矩形AEFG,点D的旋转路径为$\widehat{DG}$,若AB=1,BC=2,则阴影部分的面积为( )
如图,将矩形ABCD绕点A逆时针旋转90°至矩形AEFG,点D的旋转路径为$\widehat{DG}$,若AB=1,BC=2,则阴影部分的面积为( )| A. | $\frac{π}{3}$+$\frac{\sqrt{3}}{2}$ | B. | 1+$\frac{\sqrt{3}}{2}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{3}$+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. | 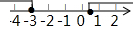 | C. |  | D. | 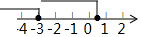 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
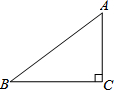 如图,一张三角形纸片ABC,其中∠C=90°,AC=6,BC=8.小静同学将纸片做两次折叠:第一次使点A落在C处,折痕记为m;然后将纸片展平做第二次折叠,使点A落在B处,折痕记为n.则m,n的大小关系是m>n.
如图,一张三角形纸片ABC,其中∠C=90°,AC=6,BC=8.小静同学将纸片做两次折叠:第一次使点A落在C处,折痕记为m;然后将纸片展平做第二次折叠,使点A落在B处,折痕记为n.则m,n的大小关系是m>n.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com