
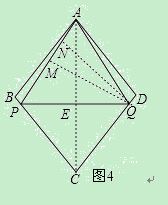
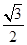 ����֤����ABC�ǡ����������Ρ���
����֤����ABC�ǡ����������Ρ���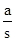 ��ֵ��
��ֵ��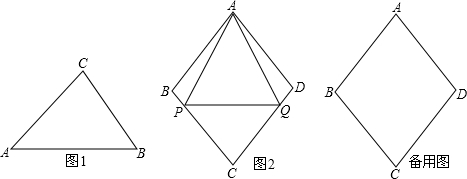
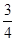 ��
��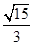 ��tan�£�2
��tan�£�2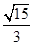 ʱ��ʹ�á�APQ��Ϊ�����������Ρ��ĸ���Ϊ2��
ʱ��ʹ�á�APQ��Ϊ�����������Ρ��ĸ���Ϊ2��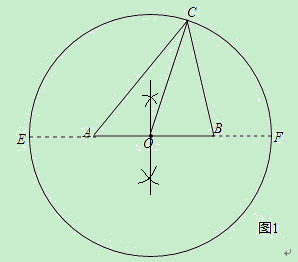

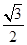 ��
��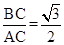
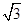 x����AC=2x��
x����AC=2x��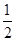 AC=x
AC=x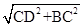 =
= 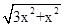 =2x��
=2x��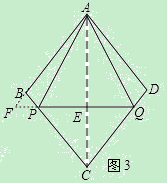
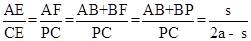 ��
��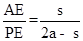 ��
��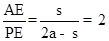 ��
��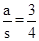 ��
��
 MP��
MP��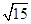 MN��
MN��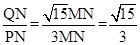 ��
��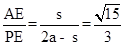 ��
��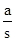 =
= 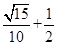
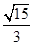 ��tan�£�2ʱ������ֻ��һ����APQ�ܳ�Ϊ�����������Ρ���
��tan�£�2ʱ������ֻ��һ����APQ�ܳ�Ϊ�����������Ρ���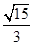 ʱ��ʹ�á�APQ��Ϊ�����������Ρ��ĸ���Ϊ2��
ʱ��ʹ�á�APQ��Ϊ�����������Ρ��ĸ���Ϊ2��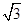 x�����������������AC=2x�������Ǻ����������BD=2x���Ӷ��ó�AC=BD���Ӷ��ó����ۣ�
x�����������������AC=2x�������Ǻ����������BD=2x���Ӷ��ó�AC=BD���Ӷ��ó����ۣ�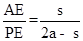 ���ٷ�������ۣ���AE=PQ��AP=QMʱ�����
���ٷ�������ۣ���AE=PQ��AP=QMʱ�����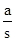 ��ֵ��
��ֵ��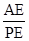 ��ֵ�������tan�µ�ȡֵ��Χ��
��ֵ�������tan�µ�ȡֵ��Χ��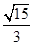 ʱ��ʹ�á�APQ��Ϊ�����������Ρ��ĸ���Ϊ2���������⣮
ʱ��ʹ�á�APQ��Ϊ�����������Ρ��ĸ���Ϊ2���������⣮

 ѧ���쳵�����ּ��ں�����ҵϵ�д�
ѧ���쳵�����ּ��ں�����ҵϵ�д� ��˼ά������ҵϵ�д�
��˼ά������ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
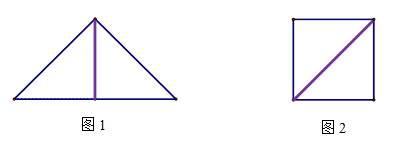
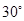 ��ǡ�ÿ���ƴ����һ������30��ǵ�ֱ�������Σ���ô��ԭ��������������ֽƬ�У��ϴ�����С��ֽƬ�����Ʊ�Ϊ________���뻭��ƴ�ӵ�ʾ��ͼ��
��ǡ�ÿ���ƴ����һ������30��ǵ�ֱ�������Σ���ô��ԭ��������������ֽƬ�У��ϴ�����С��ֽƬ�����Ʊ�Ϊ________���뻭��ƴ�ӵ�ʾ��ͼ��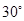 ��ֱ��������ֽƬƴ�ɣ����㻭�����ֲ�ͬƴ����ʾ��ͼ����ƴ��������ε��������У���ÿ��ƴ������С�������ε�б�߳�Ϊ
��ֱ��������ֽƬƴ�ɣ����㻭�����ֲ�ͬƴ����ʾ��ͼ����ƴ��������ε��������У���ÿ��ƴ������С�������ε�б�߳�Ϊ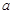 ����ֱ��д��ÿ��ƴ������������ε�б�߳���
����ֱ��д��ÿ��ƴ������������ε�б�߳����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
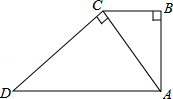
| A��2:3 | B��2:5 | C��4:9 | D��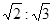 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 CEʱ��EP+BP=__________��
CEʱ��EP+BP=__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 AB����E��F�ֱ�ΪAB��AD���е㣬���AEF������BCDFE�����֮��Ϊ (����)
AB����E��F�ֱ�ΪAB��AD���е㣬���AEF������BCDFE�����֮��Ϊ (����)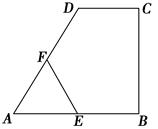
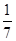 B.
B.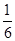 C.
C.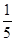 D.
D.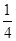
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
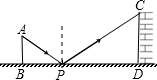
| A��6�� | B��8�� | C��18�� | D��24�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com