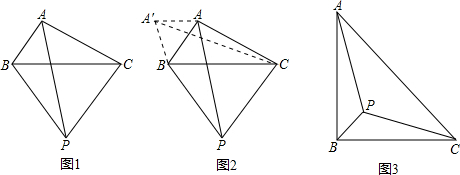
解:(1)如图,连接PP′,
将△BPC绕C点顺时针旋转60°到△AP′C的位置,由旋转的性质,得CP=CP′,
∴△PP′C为等边三角形,
由旋转的性质可知∠AP′C=∠BPC=150°,
∴∠AP′P=150°-60°=90°,
又∵PP′=PC=1,AP′=BP=2,
∴在Rt△APP′中,由勾股定理,得PA=
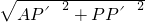
=

;
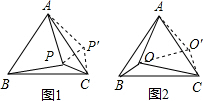
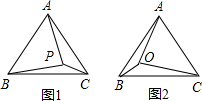
(2)以点A为中心,将△AOB逆时针旋转60°得△AO′C,
则△AO′C≌△AOB.
∴O′C=OB.连接OO′,
知△AOO′为等边三角形.
则OO′=OA,
∴△OO′C为以OA、OB、OC为边组成的三角形,
∵∠AOB:∠BOC:∠AOC=6:5:4,∠AOB+∠BOC+∠AOC=360°,
∴∠AOB=144°,∠BOC=120°,∠AOC=96°,
∵△AOO′为等边三角形,
∴∠COO′=96°-60°=36°,∠CO′O=∠CO′A-60°=∠AOB-60°=84°,
∠OCO′=180°-36°-84°=60°,
∴∠OCO′:∠COO′:∠CO′O=5:3:7.
分析:(1)根据等边三角形的性质,将△BPC绕C点顺时针旋转60°到△AP′C的位置,可证△PP′C为等边三角形,由旋转的性质可知∠AP′C=∠BPC=150°,从而可得∠AP′P=90°,PP′=PC=1,已知AP′=BP=2,在Rt△APP′中,由勾股定理可求PA;
(2)如图②,将△AOB绕A点逆时针旋转60°到△AO′C的位置,由旋转的性质可知OA=OO′,OB=CO′,故以OA、OB、OC为边组成的三角形为△OO′C,再根据已知条件求△OO′C的各内角即可.
点评:本题利用了旋转的性质解题.关键是根据AB=BC,∠ABC=60°,得出等边三角形,运用勾股定理逆定理得出直角三角形.

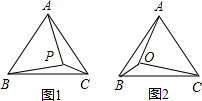 :4.求在以OA、OB、OC为边的三角形中,此三边所对的角度之比.
:4.求在以OA、OB、OC为边的三角形中,此三边所对的角度之比. 解:(1)如图,连接PP′,
解:(1)如图,连接PP′,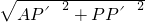 =
= ;
;

 :4.求在以OA、OB、OC为边的三角形中,此三边所对的角度之比.
:4.求在以OA、OB、OC为边的三角形中,此三边所对的角度之比.