
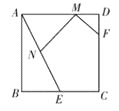
【题目】如图,在正方形ABCD中,AB=4,E是BC边的中点, F是CD边上的一点, 且DF=1.若M、N分别是线段AD、AE上的动点,则MN+MF的最小值为________.
【答案】![]()
【解析】
作点F关于AD的对称点G,过点G作GN⊥AE于点N,交AD于点M,可证得MG=MF,△MDG≌△MDF,DF=DG=1 ,可推出MN+MF=NG,根据垂线段最短,可知此时MN+MF的最小值就是NG的长;利用正方形的性质,可求出BE的长,同时可以推出∠B=∠ANM=∠FDM,∠AMN=∠BAE=∠FMD,再利用有两组对应角相等的三角形相似,可证得△ABE∽△MNA∽△FMD,然后利用相似三角形的性质及勾股定理就可求出MN,MG的长,由此看求出NG的长.
作点F关于AD的对称点G,过点G作GN⊥AE于点N,交AD于点M,
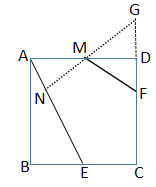
∴MG=MF,△MDG≌△MDF,DF=DG=1
∴∠GMD=∠DMF
∴MN+MF=MN+MG=NG
根据垂线段最短,可知此时MN+MF的最小值就是NG的长.
∵正方形BCD,点E是BC的中点
∴BE=![]() BC=
BC=![]() AB=2
AB=2
∴∠B=∠ANM=∠FDM=90°,∠BAE+∠MAN=90°,
∵∠AMN+∠MAN=90°,
∴∠AMN=∠BAE,
∵∠AMN=∠DMG
∴∠AMN=∠BAE=∠FMD
∴△ABE∽△MNA∽△FMD
∴![]() 即
即![]()
解之:MD=2,
∴AM=AD-MD=4-2=2
∴![]()
设AN=x,则MN=2x
∴AN2+MN2=AM2,
∴x2+4x2=4
解之:AN=x=![]()
∴MN=2AN=![]() ;
;
在Rt△MDG中,MG=![]()
∴NG=MN+MG=![]() .
.
故答案为:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
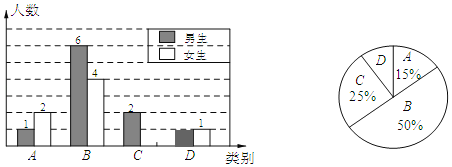
【题目】李老师为了解某校学生完成数学课前预习的具体情况,对部分学生进行了跟踪调查,并将调查结果分为四类,A:很好;B:较好;C:一般;D:较差.绘制成如下统计图.
(1)李老师一共调查了多少名同学?并将下面条形统计图补充完整.
(2)若该校有1000名学生,则数学课前预习“很好”和“较好”总共约多少人?
(3)为了共同进步,李老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习,求出所选两位同学恰好是一位男同学和一位女同学的概率.(要求列表或树状图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() ,
,![]() ,点
,点![]() 是
是![]() 轴上点
轴上点![]() 右侧一点,以
右侧一点,以![]() ,
,![]() 为两边的菱形
为两边的菱形![]() 的顶点
的顶点![]() 落在反比例函数
落在反比例函数![]() 的图象上.
的图象上.
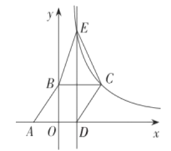
(1)求反比例函数的表达式;
(2)过点![]() 作
作![]() 轴的垂线,交反比例函数的图象于点
轴的垂线,交反比例函数的图象于点![]() ,连接
,连接![]() ,
,![]() ,求
,求![]() 的面积:
的面积:
(3)当![]() 时,请直接写出
时,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在正方形![]() 中,
中,![]() 在
在![]() 上从
上从![]() 向
向![]() 运动,连接
运动,连接![]() 交
交![]() 于
于![]() 连接
连接![]() .
.
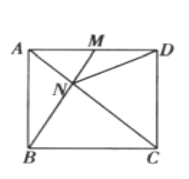
(1)证明:无论![]() 运动到
运动到![]() 上的何处,都有
上的何处,都有![]() ;
;
(2)当![]() 运动到何处时,
运动到何处时,![]() ?
?
(3)若![]() 从
从![]() 到
到![]() 再从
再从![]() 到
到![]() ,在整个运动过程中,
,在整个运动过程中,![]() 为多少时,
为多少时,![]() 是等腰三角形?
是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】上周六上午![]() 点,小颖同爸爸妈妈一起从西安出发回安康看望姥姥,途中他们在一个服务区休息了半小时,然后直达姥姥家,如图,是小颖一家这次行程中距姥姥家的距离
点,小颖同爸爸妈妈一起从西安出发回安康看望姥姥,途中他们在一个服务区休息了半小时,然后直达姥姥家,如图,是小颖一家这次行程中距姥姥家的距离![]() (千米)与他们路途所用的时间
(千米)与他们路途所用的时间![]() (时)之间的函数图象,请根据以上信息,解答下列问题:
(时)之间的函数图象,请根据以上信息,解答下列问题:
(1)求直线![]() 所对应的函数关系式;
所对应的函数关系式;
(2)已知小颖一家出服务区后,行驶![]() 分钟时,距姥姥家还有
分钟时,距姥姥家还有![]() 千米,问小颖一家当天几点到达姥姥家?
千米,问小颖一家当天几点到达姥姥家?
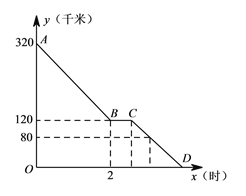
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文具店有三种品牌的6个笔记本,价格是4,5,7(单位:元)三种,从中随机拿出一个本,已知![]() (一次拿到7元本)
(一次拿到7元本)![]() .
.
(1)求这6个本价格的众数.
(2)若琪琪已拿走一个7元本,嘉嘉准备从剩余5个本中随机拿一个本.
①所剩的5个本价格的中位数与原来6个本价格的中位数是否相同?并简要说明理由;
②嘉嘉先随机拿出一个本后不放回,之后又随机从剩余的本中拿一个本,用列表法求嘉嘉两次都拿到7元本的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校准备组织一次“研学之旅”活动,现用抽签的方式从以下四个地方:九峰公园、柑橘博览园、平田桐树坑、长潭水库(其中九峰公园、平田桐树坑是爱国主义教育基地)中确定两个作为活动地点.将四个地点分别写在4张完全相同的卡片上,背面朝上并洗匀,先从中随机抽取一张卡片,再从剩下的卡片中随机抽取一张.则“抽中的两个地方都是爱国主义教育基地”的概率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华优秀传统文化,某校组织了“古诗词”知识竞赛,由九年级的若干名学生参加选拔赛,从中选出10名优胜者,下面是对参赛学生成绩的不完整统计.
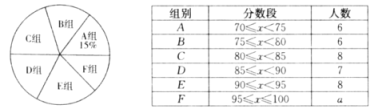
(1)统计表中,![]() =_____;各组人数的中位数是_____;统计图中,
=_____;各组人数的中位数是_____;统计图中,![]() 组所在扇形的圆心角是_____°;
组所在扇形的圆心角是_____°;
(2)李明同学得了88分,他说自己在参加选拔赛的同学中属于中午偏上水平,你认为他说的有道理吗?为什么?
(3)选出的10名优胜者中,男生、女生的分布情况如下表.
一班 | 二班 | 三班 | 四班 | 五班 | 六班 | |
男生人数 | 1 | 1 | 2 | 1 | 0 | 0 |
女生人数 | 1 | 0 | 0 | 2 | 1 | 1 |
若从中任选1名男生和1名女生代表学校参加全区的比赛,请有列表法或画树状图法求男生和女生都出在四班的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com