
分析 (1)将特殊角的三角函数值代入求解;
(2)将特殊角的三角函数值代入求解.
解答 解:(1)原式=$\frac{\frac{\sqrt{2}}{2}+\frac{\sqrt{3}}{2}}{3-1}$-$\frac{\sqrt{3}}{2}$(1-$\frac{1}{2}$)
=$\frac{\sqrt{2}}{4}$+$\frac{\sqrt{3}}{4}$-$\frac{\sqrt{3}}{4}$
=$\frac{\sqrt{2}}{4}$;
(2)原式=$\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}-\frac{\sqrt{2}}{2}}$-($\sqrt{3}$-1)-1
=$\sqrt{3}$+$\sqrt{2}$-$\sqrt{3}$
=$\sqrt{2}$.
点评 本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 起床方式 | 人数 |
| 别人叫醒 | 172 |
| 闹钟 | 88 |
| 自己醒来 | 64 |
| 其它 | 76 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
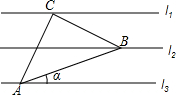 已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个项点分别在这三条平行直线上,则sinα的值是$\frac{\sqrt{10}}{10}$.
已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个项点分别在这三条平行直线上,则sinα的值是$\frac{\sqrt{10}}{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
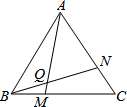 如图,已知△ABC中,AB=BC=AC,∠ABC=∠BCA=∠CAB=60°,M、N分别在△ABC的BC、AC边上,且BM=CN,AM、BN交于点Q.求证:∠BQM=60°.
如图,已知△ABC中,AB=BC=AC,∠ABC=∠BCA=∠CAB=60°,M、N分别在△ABC的BC、AC边上,且BM=CN,AM、BN交于点Q.求证:∠BQM=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com